qwertyuiop23
- 9
- 0
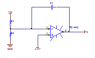
I have attached a picture of the circuit in which I am attempting to build a transfer function for, however, as you can see it is not a normal integrator. Normally it is evident which resistor is the resistor that is part of the series connection to the op amp.
When I do the KVL on the circuit to get the values I get the following function
<br /> <br /> v_{in} = C\frac{dv_{o}}{dt} + 2.5\times R_1 (\frac{1}{R1} + \frac{1}{R_2})
assuming that I voltage divide to 2.5V using values for R_1 = 5k\Omega R_2 = 910\Omega and the input is 16.3V.
<br /> v_{in} = C\frac{dv_{o}}{dt} + 16.23
From here I do not know how to get the transfer function. I am correct in assuming that the transfer function is no longer a linear line on the Bode plot due to that extra resistor that goes from the input to ground (thus reducing the current).
Or am I way off base with my assumptions.
Thank-you for your help
Lance
PS: I am an undergrad electrical engineer so the explanation does not have to be overly simplified.
When I do the KVL on the circuit to get the values I get the following function
<br /> <br /> v_{in} = C\frac{dv_{o}}{dt} + 2.5\times R_1 (\frac{1}{R1} + \frac{1}{R_2})
assuming that I voltage divide to 2.5V using values for R_1 = 5k\Omega R_2 = 910\Omega and the input is 16.3V.
<br /> v_{in} = C\frac{dv_{o}}{dt} + 16.23
From here I do not know how to get the transfer function. I am correct in assuming that the transfer function is no longer a linear line on the Bode plot due to that extra resistor that goes from the input to ground (thus reducing the current).
Or am I way off base with my assumptions.
Thank-you for your help
Lance
PS: I am an undergrad electrical engineer so the explanation does not have to be overly simplified.