DrChinese
Science Advisor
Homework Helper
Gold Member
- 8,498
- 2,130
David Byrden said:1. It can't be placed in a dark band. ... I really don't understand this comment.
I intended to put the lens near the center of the illuminated area, but really, I think that the whole area illuminated by interference bands will get light when the interference is not present.
Where is the "spot that wouldn't get any light if there were no interference" ?
2. No, that's not how telescopes work.
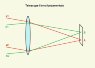
1. When there is interference, there are bands that appear strongly that do not much appear otherwise (when there is no interference, you are not investigating the "no interference" case). So this is where you will place a telescope. You hope to "resolve" the one true path, as you believe there secretly exists which-slit information that your telescope can detect.
2. That's not how light travels. There will be only 1 path through the telescope, not 2. That's because it arrives at a point when it enters the telescope. That point being a place where there is interference from the 2 slits. One effective path to your eye. Keep in mind that if there is interference, by definition it did not go through one slit or the other. It went through "both"*.*Unless you are a Bohmian.