solve the easier problem:
##\mathbf X:= \mathbf A + \mathbf I##
We can view this directly as a change of variables for the minimal polynomial
## \mathbf A^{m} + \binom{m-1}{1}\mathbf A^{m-1} + \binom{m-1}{2}\mathbf A^{m-2} + \binom{m-1}{3}\mathbf A^{m-3} +...+ \mathbf A = \Big(\big(\mathbf A + \mathbf I\big) - \mathbf I \Big)\Big(\mathbf A +\mathbf I\Big)^{m-1} = \Big(\mathbf X - \mathbf I \Big)\Big(\mathbf X\Big)^{m-1}##
## = \Big(\mathbf X\Big)^{m-1} \Big(\mathbf X - \mathbf I \Big) ##The rest of this problem ignores ##\mathbf A## and talks in terms of ##\mathbf X##
So, we focus on
##\mathbf X = \left[\begin{matrix}
1- p_{} & 1 - p_{}& 1 - p_{} & \dots &1 - p_{} &1 - p_{} & 1 - p_{}
\\p_{} & 0&0 &\dots & 0 & 0 & 0
\\0 & p_{}&0 &\dots & 0 & 0 & 0
\\0 & 0& p_{}&\dots & 0 & 0 & 0
\\0 & 0&0 & \ddots & 0&0 &0
\\0 & 0&0 & \dots & p_{}&0 &0
\\0 & 0&0 & \dots &0 & p_{} & p_{}
\end{matrix}\right]##
notice that ##\mathbf X## is the matrix associated with a (column stochastic) Markov chain.
- - - -
Plan of Attack:
Step 1:
Easiest thing first: a quick scan of the diagonal tells us that ##\text{trace}\big(\mathbf X\big) = (1-p) + p = 1##. The second step will confirm that the only possible eigenvalues of ##\mathbf X## are zeros and ones hence the trace tells us that the algebraic multiplicity of eigenvalue = 1, is one, and the algebraic multiplicity of eigenvalue 0 is ##m -1##.
Step 2:
show ##\mathbf X## is annihilated by a polynomial consisting only of roots of zeros and ones -- hence those are the only possible eigenvalues of ##\mathbf X##. In particular we are interested in the polynomial
##\mathbf X^m - \mathbf X^{m-1} = \mathbf X^{m-1}\big(\mathbf X - \mathbf I\big) = \mathbf 0##
with a slight refinement at the end we show that the above annihilating polynomial must in fact be the minimal polynomial.
- - - - -
Proof of the annihilating polynomial
note that ##\mathbf X## is a (column stochastic) matrix for a Markov chain. The idea here is to make use of the graph structure and a well chosen basis.
We seek to prove here that
##\mathbf X^m - \mathbf X^{m-1} = \mathbf X^{m-1}\big(\mathbf X - \mathbf I\big) = \big(\mathbf X -0\mathbf I\big)^{m-1}\big(\mathbf X - \mathbf I\big) = \mathbf 0##
or equivalently that
##\mathbf X^m = \mathbf X^{m-1}##
We proceed to do this one vector at a time by showing
## \mathbf s_k^T \mathbf X^m = \mathbf s_k^T \mathbf X^{m-1}##
for ##m## well chosen row vectors.
first, consider
##\mathbf s_m := \mathbf 1##
the ones vector is a left eigenvector of ##\mathbf X##, with eigenvalue of 1, which gives us
##\mathbf 1^T= \mathbf 1^T \mathbf X = \mathbf 1^T \mathbf X^2 = \mathbf 1^T \mathbf X^3 = ... = \mathbf 1^T \mathbf X^{m-1} = \mathbf 1^T \mathbf X^{m}##
This is so easy to work with, it suggests that we may be able to build an entire proof by using it as a base case of sorts.
The key insight is to then view everything in terms of the underlying directed graph. Let's consider reversing the transition diagram associated with the markov chain, and ignore re-normalization that would typically be done when trying to reverse a markov chain. (Equivalently, we're just transposing our matrix and no longer calling it a markov chain.)
- - - -
edit: the right way to state this is to say we are not using our matrix as a transition matrix but instead as an expectations operator (which is naturally given by the transpose).
- - - -
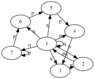
for illustrative purposes, consider the ##m :=7## case. Literally interpreted our backwards walk has a transition diagram that looks like this:
(note for graphics formatting, ##1-p## was not rendering properly, so ##q:= 1-p## has been used in the above)
But there is some special structure about dealing with the ones vector (equivalently, being in a uniform un-normalized distribution). And looking at the above diagram we can see that node 7 has rather different behavior than the others, so let's ignore it for the moment.
With just a small bit of insight, we can re-interpret the interesting parts of the state diagram as
If this is not clear to people, I'm happy to discuss more. If one 'gets' this state diagram, and recognizes that the above states can form a basis, the argument that follows for how long it takes to 'wipe out' the embedded nilpotent matrix becomes stunningly obvious. The below symbol manipulation is needed to make the argument complete, but really the above picture
is the argument for the minimal polynomial.- - - - -
Some bookkeeping to finish it off:
With these ideas in mind, now consider standard basis vectors ##\mathbf e_i##
##\mathbf s_i := \mathbf e_i## for ##i \in \{1, 2, ..., m-1\}##
the end goal is to evaluate each vector in
##\mathbf S^T =
\bigg[\begin{array}{c|c|c|c|c}
\mathbf e_1 & \mathbf e_2 &\cdots & \mathbf e_{m-1} & \mathbf 1
\end{array}\bigg]^T##
(recall: we have already done it for the ones vector)
This ##\text{m x m}## matrix is triangular with ones on the diagonal and hence invertible. After iterating through the following argument, we'll have##\mathbf S^T \mathbf X^{m} = \mathbf S^T \mathbf X^{m-1}##
or
##\mathbf X^{m} = \big(\mathbf S^T\big)^{-1} \mathbf S^T \mathbf X^{m} = \big(\mathbf S^T\big)^{-1}\mathbf S^T \mathbf X^{m-1} = \mathbf X^{m-1}##the remaining steps thus are to confirm the relation holds for ##\mathbf e_i##
for ##i=1## we have
## \mathbf e_1^T \mathbf X = (1-p) \mathbf 1^T##
and
## \mathbf e_1^T \mathbf X^2 = (1-p) \mathbf 1^T\mathbf X = (1-p) \mathbf 1^T##
hence
##\mathbf e_1^T \mathbf X = \mathbf e_1^T \mathbf X^2##
multiplying each side by ##\mathbf X^{m-2}## gives the desired result.
To chain on the end result, by following the graph, for ## 2 \leq r \leq m-1##
##\mathbf e_{r}^T \mathbf X = (p) \mathbf e_{r-1}^T##
hence
##\mathbf e_{r}^T \mathbf X^2 = (p)^2 \mathbf e_{r-2}^T##
##\vdots##
##\mathbf e_{r}^T \mathbf X^{r-1} = (p)^{r-1} \mathbf e_{1}^T##
##\mathbf e_{r}^T \mathbf X^r = (p)^{r-1}(1-p) \mathbf 1^T##and
##\mathbf e_{r}^T \mathbf X^{r +1} = \big(\mathbf e_{r}^T \mathbf X^r\big) \mathbf X = \big((p)^{r-1}(1-p) \mathbf 1^T\big) \mathbf X = (p)^{r-1}(1-p) \big(\mathbf 1^T \mathbf X\big) = \big((p)^{r-1}(1-p) \mathbf 1^T\big) = \mathbf e_{r}^T \mathbf X^r ##
if ##r = m-1## we have the desired equality.
- - - -
now to consider the ##r \lt m-1## case,
we right mutliply each side by ##\mathbf X^{(m-1) -r}## and get
## \mathbf e_{r}^T \mathbf X^{m}= \big(\mathbf e_{r}^T \mathbf X^{r+1}\big)\mathbf X^{(m-1) -r} = \big(\mathbf e_{r}^T \mathbf X^{r}\big)\mathbf X^{(m-1) -r} = \mathbf e_{r}^T \mathbf X^{m-1}##collecting all these relationships gives us
##\begin{bmatrix}
\mathbf e_1^T \\
\mathbf e_2^T \\
\vdots\\
\mathbf e_{m-1}^T \\
\mathbf 1^T
\end{bmatrix}\mathbf X^m = \begin{bmatrix}
\mathbf e_1^T \\
\mathbf e_2^T \\
\vdots\\
\mathbf e_{m-1}^T \\
\mathbf 1^T
\end{bmatrix}\mathbf X^{m-1}##
which proves the stated annihilating polynomial.
Combined with our knowledge of the trace (and Cayley Hamilton), we know that the below is the characteristic polynomial of ##\mathbf X##
##p\big(\mathbf X\big) = \mathbf X^m - \mathbf X^{m-1} = \mathbf X^{m-1}\big(\mathbf X - \mathbf I\big) = \mathbf 0##- - - -
A slight refinement: it is worth remarking here that there are some additional insights to be gained from the ##r = m-1## case. In particular we can see the imprint of the minimal polynomial as this ##r = m-1## case takes longest for the implicit walk on the graph to 'get to' the uniform state.
That is (and again, considering the picture of the graph is highly instructive here), if we consider the case of
##\mathbf e_{r}^T \mathbf X^{r-1} = (p)^{r-1} \mathbf e_{1}^T ##
and set ##r := m-1##, then we have
##\mathbf e_{m-1}^T \mathbf X^{m-2} = (p)^{m-2} \mathbf e_{1}^T \neq (p)^{m-2}(1-p) \mathbf 1^T = \mathbf e_{m-1}^T \mathbf X^{m-1}##
we have thus found
##\mathbf e_{m-1}^T \mathbf X^{m-2}\neq \mathbf e_{m-1}^T \mathbf X^{m-1}##
which means in general
## \mathbf X^{m-2} \neq \mathbf X^{m-1}##
(i.e. if the above were an equality it would have to hold for
all vectors including ##\mathbf e_{m-1}^T##)
This also means that ## \mathbf X^{m-2}\big(\mathbf X - \mathbf I\big)= \mathbf X^{m-1} - \mathbf X^{m-2} \neq \mathbf 0## which rules out a minimal polynomial of degree ##m-1##, which
also means that an even lower degree polynomial cannot annhiliate ##\mathbf X##. This point alone, confirms that the degree of the minimal polynomial must match that of the characteristic polynomial, which completes the problem.