Internal Force Diagram for Rigid Body and Distributed Load

[hdp12]

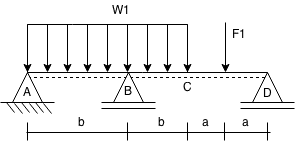
I'm working on a homework problem for Statics and I'm stuck. Could someone please help?Problem: Draw the internal force (N,V,M) diagrams and include all significant figures

Here is all of my work:

Resulting F from W₁:​

W(x) = W₁
∴ F₂=∫₀^2b W₁dx

eq (1) ⇒ F₂ = W₁⋅2b​

x₁ = (F₁)^-1 ∫₀^2b W₁dx = 1/(W₁⋅2b)⋅(W₁/2 ⋅ x²) |₀^2b

eq (2) ⇒ x₁ = b;​

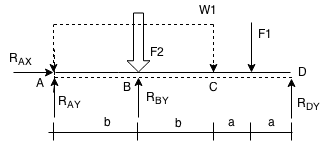
SUPPORT REACTIONS DIAGRAM &FBD:​

DIAGRAM:

FBD:

SUPPORT REACTIONS VARIABLE SOLUTION:​

[+→]∑F_x = 0 : 0 = R_AX

eq (3) ⇒ R_AX = 0 ;​

[+∧]∑F_y = 0 : 0 = (R_AY + R_BY + R_DY) - (F₁ + F₂)

eq (4) ⇒ R_AY + R_BY + R_DY = F₁ + W₁⋅2b;​

[+CW]∑M_A = 0 : 0 = (F₂⋅b + F₁(2b + a)) - (R_BY⋅b + R_DY(2b+2a))
→R_BY⋅b + R_DY(2b+2a) = W₁⋅2b⋅b + F₁(2b + a)

eq (5) ⇒ R_BY⋅b + R_DY(2b+2a) = 2⋅W₁⋅b² + F₁(2b + a) ;​

[+CW]∑M_B = 0 : 0 = (R_AY⋅b + F₁(b+a)) - R_DY(b+2a)

eq (6) ⇒ R_DY(b+2a) = R_AY⋅b + F₁(b+a) ;​

[+CCW]∑M_B = 0 : 0 = (F₁⋅a + F₂(2a+b)) - (R_BY(2a+b)+R_AY(2b+2a))

eq (7) ⇒ R_BY(2a+b)+R_AY(2b+2a) = F₁⋅a + F₂(2a+b) ;​

SEPARATE FBDs:

I:

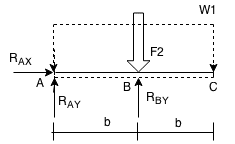II:

​

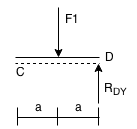
Separating the system at the hinge (C) will allow us to solve for the support reactions: In Figure 1, we can solve for the support reactions in the separate part, and therefore solve for the support reactions in the whole beam.

[+CW]∑M_B = 0 : 0 = R_AY⋅b

eq (8) ⇒ R_AY = 0 ;​

[+∧]ΣF_y = 0 : 0 = R_AY + R_BY - F₂

eq (9) ⇒ R_BY = F₂​

So now, using eq's (8) & (9) in eq (4) we can determine R_DY
eq (4) : R_AY + R_BY + R_DY = F₁ + W₁⋅2b
→F₂ + R_DY = F₁ + W₁⋅2b
→ R_DY = F₁ + W₁⋅2b - W₁⋅2b

eq (10) ⇒ R_DY = F₁​

(9) > (5) : F₂⋅b + R_DY(2b+2a) = 2⋅W₁⋅b² + F₁(2b + a)
→ R_DY(2b+2a) = 2⋅W₁⋅b² + F₁(2b + a) - (W₁⋅2b)⋅b
→ R_DY= 1/(2b+2a)[F₁(2b + a) + 2⋅W₁⋅b² - (W₁⋅2b)⋅b]
→ R_DY= F₁(2b + a)/(2b+2a)I'm just super lost, I guess, on where to go and if I'm even starting in the right direction... could someone please help me?

 

[haruspex]

Are you sure you are intpreting W₁ correctly? You are taking it as the weight per unit length. From the info in the OP, it could just as easily be the total weight (your F₂).
Your first eqn for x₁ has some typos, but it worked out ok.
When you considered the hinged parts separately, you overlooked that there may be a force at C between the two parts. Your eqn 10 is clearly wrong if you consider moments about C.

 

[hdp12]

Are you sure you are intpreting W₁ correctly? You are taking it as the weight per unit length. From the info in the OP, it could just as easily be the total weight (your F₂).
Your first eqn for x₁ has some typos, but it worked out ok.
When you considered the hinged parts separately, you overlooked that there may be a force at C between the two parts. Your eqn 10 is clearly wrong if you consider moments about C.

Yes W₁'s units are Force/Distance.
what are the typos for x₁, just so I know?
and

[+CCW]ΣM_C = 0 : 0 = (F₁⋅a + F₂(2a+b)) - (R_BY(2a+b)+R_AY(2b+2a))
eq (7) ⇒ R_BY(2a+b)+R_AY(2b+2a) = F₁⋅a + F₂(2a+b) ;

is supposed to be Sum of Moments at C, so considering, what do I do with this information?

 

[haruspex]

what are the typos for x1, just so I know?

$x_1 = (F_1)^{-1}\int _0^{2b} W_1dx$

Shouldn't that be $x_1 = (F_2)^{-1}\int _0^{2b} W_1x.dx$?

[+CCW]ΣM_C = 0 : 0 = (F₁⋅a + F₂(2a+b)) - (R_BY(2a+b)+R_AY(2b+2a))
is supposed to be Sum of Moments at C

Looks like moments about D to me.

 

[Chestermiller]

The key to getting the reaction forces in this problem is recognizing that the bending moment at point C is zero. I think that you noted this, but you still got the wrong values for the reaction forces.

If I do a moment balance on the portion of the beam to the right of C by taking moments about the hinge at point C, I get:
$$2aR_D-aF_1 = 0$$
This yields $R_D=F_1/2$

Now, what do you get if you do the same kind of thing for the portion of the beam to the left of point C?

(I get $R_A=-F_1/2$ and $R_B=2W_1b+F_1$)

Chet

 

[hdp12]

okay so using your logic...
[+CW]ΣM_C = 0 : 0 = F₁a - 2a⋅R_DY
→R_DY = (2a)^-1(F₁a)

⇒ R_DY = F₁/2
​

then plugging this solution for R_DY into eq (5) I get:
R_BY = 1/b (2⋅W₁⋅b² + F₁(2b+a)-R_DY(2b+2a))
→R_BY = (2⋅W₁⋅b²)/b + F₁⋅(2b+a)/b - F₁/2⋅(2b+2a)/b
→R_BY = 2⋅W₁⋅b + F₁⋅(2+a/b) - F₁⋅(1+a/b)

⇒R_BY = 2⋅W₁⋅b + F₁​

then plugging this solution for R_BY into eq (4) I get:
R_AY = F₁ + 2bW₁ - R_BY - R_DY
→R_AY = F₁ + 2bW₁ - (2bW₁ + F₁) - (F₁/2)

⇒R_AY = - F₁/2
​

Now that I have the support reactions, I should be able to determine the Internal Force equations and create a diagram from that information.

What is the best strategy to go about this?

 

[Chestermiller]

I don't know what the best strategy is. I would start at the left and work my to the right, first getting the V's, and then starting at the left again and getting the M's.

Chet