Internal resistance of multimeter

[bigplanet401]

Homework Statement

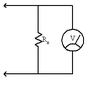
I am taking a class in circuit analysis and am trying to measure the internal resistance of the Radio Shack multimeter. The internal resistance (unknown) is R_x. A battery (with voltage V_s) is available along with a resistor R that has the same order of magnitude of R_x.

Homework Equations

Kirchhoff's voltage law (KVL)

The Attempt at a Solution

I tried using the circuit shown in the attached file and connected it in the way shown below the circuit. Before making any connections, I tried to figure out what the voltages would be.

I think the voltage across R should be V_s because of KVL around the loop containing the battery and the resistor.

By applying KVL around the loop containing the multimeter, I get the following equation:

V_x + V_s = v

(V_x is the voltage across the internal resistance of the meter.)

But when I hook up the circuit, the voltage v is less than V_s, which would mean that V_x is negative, right? This does not make sense to me. It looks like R_x and R are in series, which, if V_x was positive, would mean that I could write something like

<br /> v \frac{R}{R+R_x} = V_s<br />

which would mean

<br /> R\left( \frac{v}{V_s} - 1 \right) = R_x<br />

But because v is less than V_s, the parenthesized expression is negative and R_x is negative, which can't be true. Any advice?

 

[gneill]

You seem to be thinking of the meter resistance as being in series with a meter device which has infinite resistance. Instead, consider the meter resistance as a resistance value that is in parallel with ("shunts") a perfect meter. The perfect (or "ideal") meter tells you the potential across this meter resistance.

You might want to reconsider the configuration of your test circuit (hint: think voltage divider).

 

[Basic_Physics]

Your equation:
V_x + V_s = v
should rather read
V_s - V_x = V
The emf of the battery is positve, but the voltage drop through Rx is negative.