to819
- 8
- 0
Introductory Vector Equation Illustrated by a Moving River -- Picture Included
A swimmer wants to cross a river, from point A to point B, as shown in the figure. The distance (from A to C) is 100 , the distance (from C to B) is 75 , and the speed of the current in the river is 5 . Suppose that the swimmer's velocity relative to the water makes an angle of with the line from A to C, as indicated in the figure.
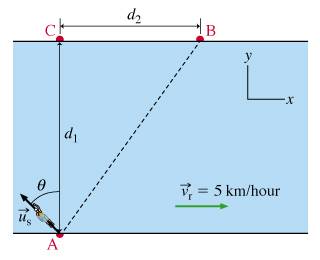 To swim directly from A to B, what speed , relative to the water, should the swimmer have?
To swim directly from A to B, what speed , relative to the water, should the swimmer have?
A to B2=1002+752
A to B= 125 meters
That's about all I really know how to do. For some reason I can't think of a way to go about solving this problem. Any ideas?
Homework Statement
A swimmer wants to cross a river, from point A to point B, as shown in the figure. The distance (from A to C) is 100 , the distance (from C to B) is 75 , and the speed of the current in the river is 5 . Suppose that the swimmer's velocity relative to the water makes an angle of with the line from A to C, as indicated in the figure.
Homework Equations
A to B2=1002+752
A to B= 125 meters
That's about all I really know how to do. For some reason I can't think of a way to go about solving this problem. Any ideas?
Last edited: