moephysics
- 17
- 0
Homework Statement
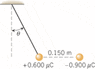
A small spherical insulator of mass 8.00x10^-2 Kg and charge 6.0x10^-5C is hung by a thin wire of negligible mass. A charge of -9.0x10^-5 is held 0.150 m away from the sphere and directly to the right of it, so the wire makes an angle with the vertical (see the drawing). Find (a) the angle and (b) the tension in the wire.
Homework Equations
Fe=Kq1q2\r^2
The Attempt at a Solution
Well as far as the tension is concerned I have no problem, I have mg and Fe and from adding them vectorialy I can figure out the tension. However when I tried to figure out the angle I tried a trigonometrical approach where I extended the line and made a big triangle and a small triangle so I can try to figure out the length L of the thin wire and one of the sides of the triangle so I can calculate the angle. However when I tried that approach I seem to be going through trouble with having less information than needed, so if someone can help give me a hint or something that could push me further, that's all and thank you (and also I have attached a picture with this thread if anyone wants the problem shown in a diagram)
Attachments
Last edited: