atha
- 7
- 1
I was given a sample, that it is suppossed to be a medium thickness Rhodium on top of an infinite silicon waffer. The experimental RBS spectrum along with the simulation looks like that
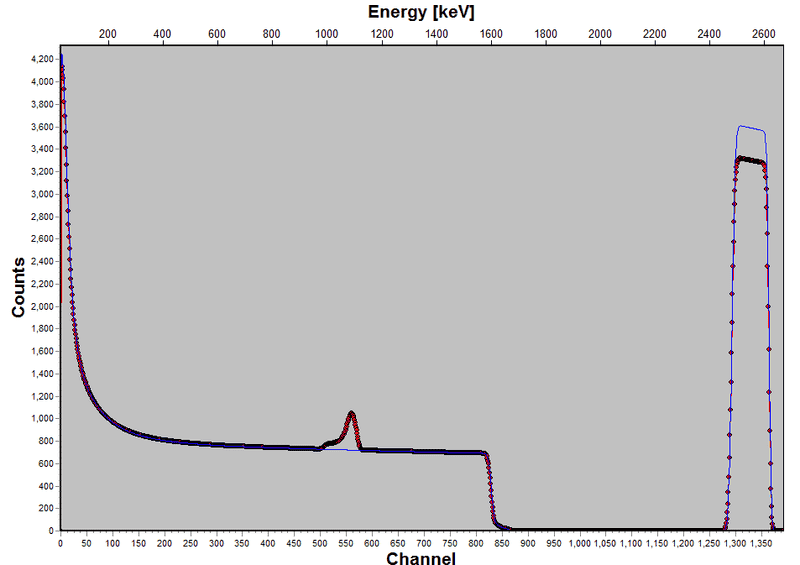
Apparently, there is another element(or maybe 2) that appear on the experimental spectrum.
I am relatively new to RBS, so I find rather confusing to see two narrow peaks, so close to each other on the substrate part of the spectrum.
If the waffer wasn't pure, I would expect some steps, rather than peaks. The way I see it, it's an indication of a possible thin and light layer of unknown elements. How to specify which elements could that be?
Is there also a way to find out if it is really another layer and its position?
On a second look, it seems that the real spectrum has less events that the simulated, which could be an indication of a non pure Rhodium sample. The question is, which element(s) is responsible for the possible impurity?
Apparently, there is another element(or maybe 2) that appear on the experimental spectrum.
I am relatively new to RBS, so I find rather confusing to see two narrow peaks, so close to each other on the substrate part of the spectrum.
If the waffer wasn't pure, I would expect some steps, rather than peaks. The way I see it, it's an indication of a possible thin and light layer of unknown elements. How to specify which elements could that be?
Is there also a way to find out if it is really another layer and its position?
On a second look, it seems that the real spectrum has less events that the simulated, which could be an indication of a non pure Rhodium sample. The question is, which element(s) is responsible for the possible impurity?