FranzDiCoccio
- 350
- 43
Hi all,
this question is related to a similar one I posted a couple of weeks back.
Please keep in mind that the level here is high school. I'm looking for a way of describing the concepts in the title that is not overly technical. I keep circling back to these concepts because it seems to me that there is something I'm missing, but I'm not able to put my finger on it.
So my question has basically to do with Carnot's principle, and reversible vs irreversible cycles.
From "Physics - 9th ed." by Cutnell and Johnson:
According to this principle, one must conclude that all reversible cycles between the same two temperatures should attain the same efficiency. Since the Carnot cycle is the prototype of reversible cycle, all reversible cycles between the same two temperatures should attain the same efficiency as the Carnot cycle.
Now in high-school textbooks I find problems about "non-Carnot" cycles. For instance, problem 29 of chapter 20 in "Fundamentals of Physics" by Halliday-Resnick/Walker shows this cycle, specifying that it is reversible,
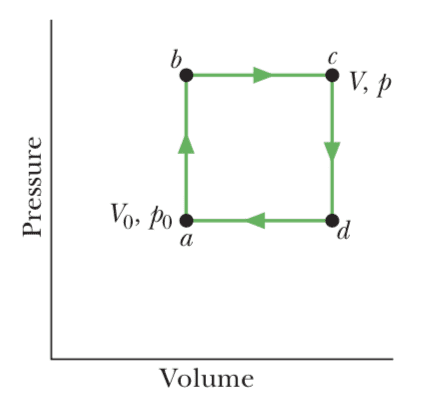 and asks the student for the work done during the cycle, the heat added during stroke abc, the efficiency of the cycle, and the efficiency of a Carnot cycle operating between the highest and lowest temperature in the cycle.
and asks the student for the work done during the cycle, the heat added during stroke abc, the efficiency of the cycle, and the efficiency of a Carnot cycle operating between the highest and lowest temperature in the cycle.
The efficiency of the cycle turns out to be (of course) less than the Carnot cycle. I'm not exactly clear about why it is not equal to it, being the cycle reversible.
One possible answer is that, in order to make that cycle reversible, heat should be exchanged gradually, i.e. via a series of "small" isothermal processes, and for that one needs many reservoirs at different constant temperatures.
If this is the case, the Carnot Principle cannot be applied to this cycle in a straightforward way, because this cycle is not "operating between two reservoirs".
Is that it?
I have further questions about this kind of situation, but I'll ask them later.
this question is related to a similar one I posted a couple of weeks back.
Please keep in mind that the level here is high school. I'm looking for a way of describing the concepts in the title that is not overly technical. I keep circling back to these concepts because it seems to me that there is something I'm missing, but I'm not able to put my finger on it.
So my question has basically to do with Carnot's principle, and reversible vs irreversible cycles.
From "Physics - 9th ed." by Cutnell and Johnson:
No irreversible engine operating between two reservoirs at constant temperatures can have a greater efficiency than a reversible engine operating between the same temperatures. Furthermore, all reversible engines operating between the same temperatures have the same efficiency
According to this principle, one must conclude that all reversible cycles between the same two temperatures should attain the same efficiency. Since the Carnot cycle is the prototype of reversible cycle, all reversible cycles between the same two temperatures should attain the same efficiency as the Carnot cycle.
Now in high-school textbooks I find problems about "non-Carnot" cycles. For instance, problem 29 of chapter 20 in "Fundamentals of Physics" by Halliday-Resnick/Walker shows this cycle, specifying that it is reversible,
The efficiency of the cycle turns out to be (of course) less than the Carnot cycle. I'm not exactly clear about why it is not equal to it, being the cycle reversible.
One possible answer is that, in order to make that cycle reversible, heat should be exchanged gradually, i.e. via a series of "small" isothermal processes, and for that one needs many reservoirs at different constant temperatures.
If this is the case, the Carnot Principle cannot be applied to this cycle in a straightforward way, because this cycle is not "operating between two reservoirs".
Is that it?
I have further questions about this kind of situation, but I'll ask them later.