Is C1*C1 Always Equal to C1 in Convolution Integrals with e^At?

[aaddcc]

Hi All,

I am taking Dynamic Systems and Controls this semester for Mechanical Engineering. We are solving non homogeneous state space equations right now. This question is about a 2x2 state space differential equation that takes the form:

Where A and B are matrices, while u is an input (like sin(t), etc). We have written this to generally be:

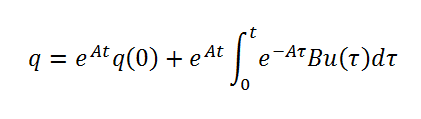
The situation I am wondering about, is when e^At is only real numbers (we use the laplace transform to solve this normally, so no sine or cosine), which means it is of the form:

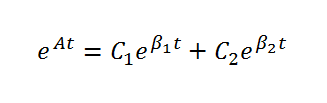
Our professor agrees that C1*C2 = 0 is always true when it is of this form, which simplifies the convolution integral significantly. Additionally, in homeworks and lecture notes I noticed that C1*C1 = C1 and C2*C2=C2. I asked the Professor if this is always true, and he commented that he's not sure if it is always but that it was for the examples we did. What do you guys think, is that always true? If so, that simplifies the convolution integral even further. I am an engineer, not a mathematician, so my memory of DiffEq and proofs isn't so good, but I thought this was an interesting question

 

[MisterX]

It's true provided $\mathbf{A}$ is a real symmetric matrix ($\mathbf{A} = \mathbf{A}^T$), or more generally a Hermitian matrix. Ideally you should understand at least some of why that is. If $\mathbf{A}$ is a real symmetric matrix, then it has an orthogonal basis of eigenvectors, and we may write
$$\mathbf{A} = \beta_1vv^T + \beta_2ww^T$$
Where $v$ and $w$ are vectors such that

$v^Tv = w ^T w = 1$
$v^Tw = w^Tv = 0$

You should verify that this means $\mathbf{A}v = \beta_1 v$ and $\mathbf{A}w = \beta_2 w$. Furthermore, due to the properties above,

$\mathbf{A}^2 = \beta_1^2vv^T + \beta_2^2ww^T$
$\mathbf{A}^n = \beta_1^nvv^T + \beta_2^nww^T$

Now
$$e^{\mathbf{A}t} = \sum^\infty_{n = 0} \frac{\mathbf{A}^nt^n}{n!}= 1 + \mathbf{A}t + \frac{1}{2}\mathbf{A}\mathbf{A}t^2 + ...$$
So using our formula from above,
\begin{align*} e^{\mathbf{A}t} &= \sum^\infty_{n = 0} \frac{t^n}{n!}\beta_1^nvv^T + \frac{t^n}{n!}\beta_2^nww^T \\
&= vv^T\, e^{\beta_1 t} + ww^T \, e^{\beta_2 t} \end{align*}

So, $\mathbf{C}_1 = vv^T$ and $\mathbf{C}_2 = ww^T$, and indeed
\begin{align*}\mathbf{C}_1\mathbf{C}_2 &= v(v^Tw)w^T = v0w^T = 0 \\
\mathbf{C}_1\mathbf{C}_1 &= v(v^Tv)v^T = v(1)v^T = \mathbf{C}_1 \\
\mathbf{C}_2\mathbf{C}_2 &= w(w^Tw)w^T = w(1)w^T = \mathbf{C}_2 \\
\end{align*}
But, remember we had to assume that $\mathbf{A}$ had a complete set of orthonormal eigenvectors, $\mathbf{A} = \beta_1vv^T + \beta_2ww^T$. This is true for a real symmetric matrix, which means $\mathbf{A} = \mathbf{A}^T$. For other kinds of matrices this may not hold. You will not even generally be able to write $e^{\mathbf{A}t} = C_1 e^{\beta_1t} + C_2 e^{\beta_2t}$ for other kinds of matrices.