Is electric field decomposable when detected by CCD?

[genxium]

Homework Statement

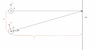
I'm learning light interference and confused by the concepts. Like the figure I attached below, while computing the "interference" of the intersection point on the CCD, I used to do this (E represents the electric field):

E_{CCD}=E_1 \cdot e^{i (\omega t + \frac{2 \pi}{\lambda} l)} + E_2 \cdot e^{i (\omega t + \frac{2 \pi}{\lambda} (l+d \cdot sin \alpha))}

I know this is wrong because electric field is directional and I should decompose it so that only components in the same direction add up -- yet I'm not sure how to do it. Does a CCD detector respect the direction of fields?

Homework Equations

Described above.

The Attempt at a Solution

Described above.

 

[rude man]

I don't know why you can't use traditional ray optics with the CCD at the location of the real image. You need to focus on a CCD just like on a screen or film. But perhaps I'm way off base here.