Is My Homework Solution Correct?

[Pushoam]

Homework Statement

Homework Equations

The Attempt at a Solution

$C_p - C_v = p \frac{\partial V}{\partial T}$
Doing the above, I got $R\{ 1+ \frac{bp} {RT^2}\}$, there is no square in the right factor.
I want to know whether my answer is correct.

 

[Chestermiller]

$C_p - C_v = p \frac{\partial V}{\partial T}$

This equation is incorrect.

 

[Pushoam]

This equation is incorrect.

How is it so?
$C_p = [\frac{\partial U}{\partial T} = C_v] +p \frac{\partial V}{\partial T}$
Isn't the above correct?
Will you please reply to the following threads,too?
Which cylinder reaches the ground first?

2nd order differential eqn.

Material: semi - conductor or metal?

 

[Chestermiller]

How is it so?
$C_p = [\frac{\partial U}{\partial T} = C_v] +p \frac{\partial V}{\partial T}$
Isn't the above correct?
Will you please reply to the following threads,too?
Which cylinder reaches the ground first?

2nd order differential eqn.

Material: semi - conductor or metal?

No. That equation is not correct. Consult your textbook for the correct equation for determining the difference between the two heat capacities.

 

[Pushoam]

C_p = [\frac{\partial U}{\partial T} = C_v] +p \frac{\partial V}{\partial T}

$\frac{\partial U}{\partial V} \frac{\partial V}{\partial T} = \frac{\partial U}{\partial T} = C_v$
How to calculate the above as U is not given?

Sorry, the above is wrong as V and T are independent variables?
U is a fn. of both V and T. Then, how to calculate $\frac{\partial U}{\partial V}$?

 

[Chestermiller]

View attachment 214682
C_p = [\frac{\partial U}{\partial T} = C_v] +p \frac{\partial V}{\partial T}

$\frac{\partial U}{\partial V} \frac{\partial V}{\partial T} = \frac{\partial U}{\partial T} = C_v$
How to calculate the above as U is not given?

Sorry, the above is wrong as V and T are independent variables?
U is a fn. of both V and T. Then, how to calculate $\frac{\partial U}{\partial V}$?

That should be in your book also.

 

[Pushoam]

That should be in your book also.

I didn't get it in the book.
I took U = pV and expressed p in terms of V.
This gives, p = $\frac {RT}{V + \frac b T }$
This gives $U = RT - \frac {bR}{V + \frac b T } \\ \frac { \partial U} {\partial V} = \frac {bR}{\{V + \frac b T\}^2 }$
After doing further calculation,
we get the option c as the correct answer.
But how to prove that U = pV? Is it valid always?

 

[Chestermiller]

I didn't get it in the book.
I took U = pV and expressed p in terms of V.
This gives, p = $\frac {RT}{V + \frac b T }$
This gives $U = RT - \frac {bR}{V + \frac b T } \\ \frac { \partial U} {\partial V} = \frac {bR}{\{V + \frac b T\}^2 }$
After doing further calculation,
we get the option c as the correct answer.
But how to prove that U = pV? Is it valid always?

It's not even valid for an ideal gas.

 

[Pushoam]

It's not even valid for an ideal gas.

Which part is not valild? Is it U = pV?
But, it gave the correct answer.

 

[Charles Link]

I was able to show with some work by expanding differentials of $U(T,P)$ and $U(T,V)$ that $C_P-C_V=P \big( \frac{\partial{V}}{\partial{T}} \big)_P +\big( \frac{\partial{U}}{\partial{P}} \big)_T \big( \frac{\partial{P}}{\partial{T}} \big)_V$. I don't know, however, how to compute $\big( \frac{\partial{U}}{\partial{P}} \big)_T$ from the information provided.

 

[Chestermiller]

Which part is not valild? Is it U = pV?

If you're going to wild ass it like this, I won't be helping you any more. Now, I'll give you one more opportunity: What does your book give as the general expression for the partial derivative of U with respect to V at constant T.

But, it gave the correct answer.

So what!

 

[Chestermiller]

I was able to show with some work by expanding differentials of $U(T,P)$ and $U(T,V)$ that $C_P-C_v=P( \frac{\partial{V}}{\partial{T}})_P +(\frac{\partial{U}}{\partial{P}})_T (\frac{\partial{P}}{\partial{T}})_V$. I don't know, however, how to compute $(\frac{\partial{U}}{\partial{P}})_T$ from the information provided.

All thermo books give a general expression in terms of P, V, and T for this partial derivative.

 

[Abhishek kumar]

Which part is not valild? Is it U = pV?
But, it gave the correct answer.

Which part is not valild? Is it U = pV?
But, it gave the correct answer.[/Q

Which part is not valild? Is it U = pV?
But, it gave the correct answer.

First

I didn't get it in the book.
I took U = pV and expressed p in terms of V.
This gives, p = $\frac {RT}{V + \frac b T }$
This gives $U = RT - \frac {bR}{V + \frac b T } \\ \frac { \partial U} {\partial V} = \frac {bR}{\{V + \frac b T\}^2 }$
After doing further calculation,
we get the option c as the correct answer.
But how to prove that U = pV? Is it valid always?

Apply this formula you will get the result

 

[Charles Link]

Thank you @Chestermiller :) I usually try to solve these (thermodynamic problems) without looking the necessary equation up in a textbook, but this one is a little more difficult. Adkins book, Equilibrium Thermodynamics, gives equation (8.4): $C_P-C_V=T \big( \frac{\partial{P}}{\partial{T}} \big)_V \big( \frac{\partial{V}}{\partial{T}} \big)_P$. $\\$ The rest was simply applying some calculus with a little algebra. (Yes, I was able to get the correct answer). $\\$ @Pushoam may also find this equation to be helpful.

 

[Chestermiller]

Thank you @Chestermiller :) I usually try to solve these (thermodynamic problems) without looking the necessary equation up in a textbook, but this one is a little more difficult. Adkins book, Equilibrium Thermodynamics, gives equation (8.4): $C_P-C_V=T \big( \frac{\partial{P}}{\partial{T}} \big)_V \big( \frac{\partial{V}}{\partial{T}} \big)_P$. $\\$ The rest was simply applying some calculus with a little algebra. (Yes, I was able to get the correct answer). $\\$ @Pushoam may also find this equation to be helpful.

Hi Charles,
I just gave another member a warning for revealing essentially what you revealed in this post, since it is essentially the complete solution. I was hoping that the OP would do research on his own to find the relationship (or the derivative of U with respect to V at constant T) in order to discourage him from making wild guesses. I suppose I'll cancel the other member's warning if I can figure out how to.

Chet

 

[Charles Link]

Hi Charles,
I just gave another member a warning for revealing essentially what you revealed in this post, since it is essentially the complete solution. I was hoping that the OP would do research on his own to find the relationship (or the derivative of U with respect to V at constant T) in order to discourage him from making wild guesses. I suppose I'll cancel the other member's warning if I can figure out how to.

Chet

Hello @Chestermiller If you are referring to post 13, it is interesting, but he doesn't show the origin of his equation, and I believe it to be incorrect. It is also dimensionally incorrect, if I'm not mistaken.

 

[Charles Link]

Apply this formula you will get the result

For the OP @Pushoam and @Abhishek kumar I believe this equation (post 13) is incorrect. See my post 14. I think the equation in post 13 is not even dimensionally correct.

 

[Chestermiller]

For the OP @Pushoam and @Abhishek kumar I believe this equation (post 13) is incorrect. See my post 14. I think the equation in post 13 is not even dimensionally correct.

Sorry to say this Charles, but I agree with the result in post #13. It is essentially the same as your result in post #14.

 

[Charles Link]

Sorry to say this Charles, but I agree with the result in post #13. It is essentially the same as your result in post #14.

My mistake with the dimensional analysis. It's going to take a little work to show the two are equivalent though.

 

[Chestermiller]

My mistake with the dimensional analysis. It's going to take a little work to show the two are equivalent though.

V=V(P,T)
dV = ??
then, set dV = 0

 

[Charles Link]

V=V(P,T)
dV = ??
then, set dV = 0

I just got the result. It's easier than I thought it would be. Will show it momentarily... $\\$ $dP=\big( \frac{\partial{P}}{\partial{T}} \big)_V dT+\big( \frac{\partial{P}}{\partial{V}} \big)_T dV$. Setting $dP=0$ allows one to take $\big( \frac{\partial{V}}{\partial{T}} \big)_P$. The hardest part was actually writing out the Latex. :)

 

[Abhishek kumar]

V=V(P,T)
dV = ??
then, set dV = 0

Dear Chestermiller posting correct formula is not allowed?i haven't posted complete solution how can you warn me?

 

[Charles Link]

Dear Chestermiller posting correct formula is not allowed?i haven't posted complete solution how can you warn me?

Please see his post #15. I can't speak for him, but I think he changed his mind. He might not have been able to cancel it.

 

[Chestermiller]

Dear Chestermiller posting correct formula is not allowed?i haven't posted complete solution how can you warn me?

Please see my message to you in a private conversation.

 

[Pushoam]

If you're going to wild ass it like this, I won't be helping you any more. Now, I'll give you one more opportunity: What does your book give as the general expression for the partial derivative of U with respect to V at constant T.So what!

I have to find out $C_P - C_V = \{\frac{\partial U} {\partial V} +p\}\frac{dV}{dT}$

For $C_V$, I have to calculate $\frac{\partial U} {\partial T}$. It is not needed to calculate $C_V$ for this problem,

but this gives me the idea that here, U is a function of two variables V and T.

Not getting how to calculate $\frac{\partial U} {\partial V}$ from dU = T dS - pdV, I thought of using Maxwell's relation.

So, I take that potential which is a function of V and T i.e. Helmholtz function F.

F = U - TS

dF = - pdV - S dT

Maxwell's relation gives,

$\frac{\partial F} {\partial T} = -S \\\frac{\partial F} {\partial V}= -p \\ \frac{\partial S} {\partial V}= \frac{\partial p} {\partial T} \\ \frac{\partial U} {\partial V} = \frac{\partial F} {\partial V} + T \frac{\partial S} {\partial V} = -p +T\frac{\partial p} {\partial T}$

Is this correct?

Thank you for discouraging me from Wild guess. Wild guess simply wastes time.Doing further calculation,

$\{\frac{\partial U} {\partial V} +p\} = p\{ 1+ \frac {bp}{RT^2} \}$

$\frac {dV}{dT}= \frac 1 p \{ 1+ \frac {bp}{RT^2} \}$
So, $C_P - C_V = \{\frac{\partial U} {\partial V} +p\}\frac{dV}{dT} = {\{ 1+ \frac {bp}{RT^2} \}}^2$
Here, I have taken U as a function of V and T. So, V and T are independent variables.

While calculating $\frac {dV}{dT}$, I have taken V as a function of T keeping p constant. Isn't it wrong?

Shouldn't I take $\frac {dV}{dT} =0$ assuming U as a function of V and T and so V and T independent variables?

 

[Charles Link]

The derivative $\big( \frac{\partial{V}}{\partial{T}} \big)_P = \frac{dV}{dT}$ should have a factor of $R$ in it. That will give you the correct answer for $C_P-C_V$. $\\$ Note: It's not really $\frac{ dV}{dT}$. $V$ is a function of two other variables=in this case $V=V(T,P )$ . $\\$ You can write $dV=\big( \frac{\partial{V}}{\partial{T}} \big)_P \, dT+ \big(\frac{ \partial{V}}{\partial{P}} \big)_T \, dP$ , but not $\frac{dV}{dT}$.

 

[Pushoam]

The derivative $\big( \frac{\partial{V}}{\partial{T}} \big)_P = \frac{dV}{dT}$ should have a factor of $R$ in it. That will give you the correct answer for $C_P-C_V$.

Yes, it has. Thanks for pointing it out.

 

[Pushoam]

Note: It's not really $\frac{ dV}{dT}$ . V is a function of two other variables=in this case V=V(T,P) You can write $\big( \frac{\partial{V}}{\partial{T}} \big)_P \, dT+ \big(\frac{ \partial{V}}{\partial{P}} \big)_T \, dP$ , but not $\frac{dV}{dT}$ .

Here, I have taken U as a function of V and T. So, V and T are independent variables.

While calculating $\frac {dV}{dT}$ , I have taken V as a function of T keeping p constant. Isn't it wrong?

Shouldn't I take $\frac {dV}{dT} =0$ assuming U as a function of V and T and so V and T independent variables?

What about this?
Sometimes V is independent, sometimes V becomes a fn. of P and T. This I find difficult to understand.

 

[Chestermiller]

I have to find out $C_P - C_V = \{\frac{\partial U} {\partial V} +p\}\frac{dV}{dT}$

For $C_V$, I have to calculate $\frac{\partial U} {\partial T}$. It is not needed to calculate $C_V$ for this problem,

but this gives me the idea that here, U is a function of two variables V and T.

Not getting how to calculate $\frac{\partial U} {\partial V}$ from dU = T dS - pdV, I thought of using Maxwell's relation.

So, I take that potential which is a function of V and T i.e. Helmholtz function F.

F = U - TS

dF = - pdV - S dT

Maxwell's relation gives,

$\frac{\partial F} {\partial T} = -S \\\frac{\partial F} {\partial V}= -p \\ \frac{\partial S} {\partial V}= \frac{\partial p} {\partial T} \\ \frac{\partial U} {\partial V} = \frac{\partial F} {\partial V} + T \frac{\partial S} {\partial V} = -p +T\frac{\partial p} {\partial T}$

Is this correct?

Thank you for discouraging me from Wild guess. Wild guess simply wastes time.

Now, that's what I was looking for. Congratulations. We're proud of you. You've transformed from a wild guesser into a Scholar. Keep up the good work.

 

[Charles Link]

In writing some of the calculations with Latex, for shorthand it can be helpful to write $\frac{dV}{dT}$, but this expression always requires the other variable to be held constant. See my edited post 26. Writing many partial derivatives with Latex is really rather difficult. It would be much easier if we had pencil and paper... To answer post 28, you can write $U=U(T,P)$, and also $U=U(T,V)$. When you write out $dU$, you get two different expressions, (see post 26), one with $dT$ and $dP$ , and the other with $dT$ and $dV$...

 

[Pushoam]

Now, that's what I was looking for. Congratulations. We're proud of you. You've transformed from a wild guesser into a Scholar. Keep up the good work.

This has made me quite happy. Thank you, thanks a lot...

 

[Pushoam]

What about this?
Sometimes V is independent, sometimes V becomes a fn. of P and T. This I find difficult to understand.

Please help me in post 28.

 

[Chestermiller]

What about this?
Sometimes V is independent, sometimes V becomes a fn. of P and T. This I find difficult to understand.

In post #5, that is a partial derivative of V with respect to T at constant P. To understand how this came about, you need to go back and study the derivation of the equation in post #5.

 

[Charles Link]

Please help me in post 28.

See edited posts 26 and 30.

 

[Chestermiller]

The derivation goes like this:

$$dH=dU+PdV+VdP=\left(\frac{\partial U}{\partial T}\right)_VdT+\left(\frac{\partial U}{\partial V}\right)_TdV+PdV+VdP$$

So, evaluating the partial derivative of H with respect to T at constant P, we have $$\left(\frac{\partial H}{\partial T}\right)_P=\left(\frac{\partial U}{\partial T}\right)_V+\left(\frac{\partial U}{\partial V}\right)_T\left(\frac{\partial V}{\partial T}\right)_P+P\left(\frac{\partial V}{\partial T}\right)_P$$
This then gives:
$$C_p-C_v=\left(\frac{\partial U}{\partial V}\right)_T\left(\frac{\partial V}{\partial T}\right)_P+P\left(\frac{\partial V}{\partial T}\right)_P$$

 

[Pushoam]

The derivation goes like this:

$dH=dU+PdV+VdP=\left(\frac{\partial U}{\partial T}\right)_VdT+\left(\frac{\partial U}{\partial V}\right)_TdV+PdV+VdP$ ... (1)

In the above eqn., U is taken as a function of V and T. So, is it correct to assume V and T as independent variables?

In the second eqn.,

$\left(\frac{\partial H}{\partial T}\right)_P=\left(\frac{\partial U}{\partial T}\right)_V+\left(\frac{\partial U}{\partial V}\right)_T\left(\frac{\partial V}{\partial T}\right)_P+P\left(\frac{\partial V}{\partial T}\right)_P$....(2)

We calculate $\frac{\partial V}{\partial T}$. This means that V is a function of two variables T and P.
Then, $\left( \frac{\partial U}{\partial V}\right)_ T = -P + T\left( \frac{\partial P}{\partial T}\right)_V$
This means that p is a function of V and T.

So, the independent variable is only T. V is an implicit function of P and T. P is an implicit function of V and T.
U is a function of V and T.
Is this correct?

 

[Chestermiller]

In the above eqn., U is taken as a function of V and T. So, is it correct to assume V and T as independent variables?

Yes. U can be expressed as a function of V and T.

In the second eqn.,

We calculate $\frac{\partial V}{\partial T}$. This means that V is a function of two variables T and P.

Yes. This is the equation of state.

Then, $\left( \frac{\partial U}{\partial V}\right)_ T = -P + T\left( \frac{\partial P}{\partial T}\right)_V$
This means that p is a function of V and T.

Yes. The latter is the equation of state also.

So, the independent variable is only T.

I don't understand what this is supposed to mean. We are trying to develop the relationship between the partial derivative of H with respect to T at constant P, and the partial derivative of U with respect to T at constant V.

V is an implicit function of P and T. P is an implicit function of V and T.
U is a function of V and T.
Is this correct?

V being a function of P and T is equivalent to P being a function of V and T. Both of these represent the equation of state. U is usually expressed as a function of V and T, although it can also be expressed as a function of P and T, or also a function of P and V.

 

[Pushoam]

What I have understood is :

The state of the system could be characterised by P, V and T.

We have a equation of state relating P,V and T.

Any two of {P,V,T} could act as independent variables depending upon our experiment and the 3rd would be the dependent variable.

U could be a function of any of the two independent variables depending upon the experiment.

Here, we have taken U as a function of V and T.

Now, the equation:

$C_P – C_V = {\left [ {\left (\left ( \frac {\partial U } {\partial V } \right) _{T} +P \right) } \left ( \frac {\partial V } {\partial T } \right) _{P} \right ] }$ ……….(1)$dQ = \left ( \frac {\partial U } {\partial T } \right) _{V} dT + \left ( \frac {\partial U } {\partial V } \right) _{T} dV + p dV$ …….(2)

In the above equation Q is a function of V and T.

$\left ( \frac {\partial Q } {\partial T } \right) _{V} = \left ( \frac {\partial U } {\partial T } \right) _{V} + 0 +0 = C_V$....(3)

The more correct formulation is:

Q itself is a physical quantity. Depending of the experiment, sometimes it could be a function of V and T or P and T i.e. whether Q is Q = Q(V,T) or Q = Q(P,T) depends upon the experiment.

When Q is a function of V and T i.e. Q = Q( V,T),

We have,

$\left ( \frac {\partial Q } {\partial T } \right) _{V} = \left ( \frac {\partial U } {\partial T } \right) _{V} + 0 +0 = C_V$....(3)

When Q is a function of P and T i.e. Q = Q( P,T),

We have,

$\left ( \frac {\partial Q } {\partial T } \right) _{P} = C_P= \left ( \frac {\partial U } {\partial T } \right) _{V} + \{ \left ( \frac {\partial U } {\partial V } \right) _{T} + p\} \left ( \frac {\partial V } {\partial T } \right) _{P}$ …….(4)

In equation 2 and 3, we have expressed both U and Q as a function of V and T.

In equation 4, we have expressed U as a function of V and T( so we have got equation 2), but we have expressed Q as a function of P and T.

Isn’t it always true that when U is a function of V and T, then Q must be a function of V and T or when Q is a function of P and T, then U must be a function of P and T?

In equation 4, we have expressed Q = Q (P,T), so the independent variables are P and T.

V is a function of P and T i.e. V = V(P,T), while U is a function of V and T i.e. U = U(V,T). Since here V is a function of P and T, U = U(V,T) = U(V(P,T), T) = U(P,T).

So, expressing U as a function of P and T,

We have,

$C_P = \left ( \frac {\partial Q } {\partial T } \right) _{P} = \left ( \frac {\partial U } {\partial T } \right) _{P} +P \left ( \frac {\partial V } {\partial T } \right) _{P}$

Then, we have to find $\left ( \frac {\partial U } {\partial T } \right) _{P}$ applying Maxwell relations upon G(P,T).

Is this correct?

 

[Pushoam]

In the following equation

dU = dQ + dW, where dW is the work done on the system.

We write, dW = -p dV, where p is the external pressure acting on the system.

While writing dW = -p dV, is it assumed that p is constant, i.e. dW = - p dV – V dp

But because of constant p , dW = -pdV

 

[Chestermiller]

What I have understood is :

The state of the system could be characterised by P, V and T.

We have a equation of state relating P,V and T.

Any two of {P,V,T} could act as independent variables depending upon our experiment and the 3rd would be the dependent variable.

U could be a function of any of the two independent variables depending upon the experiment.

Here, we have taken U as a function of V and T.

Now, the equation:

$C_P – C_V = {\left [ {\left (\left ( \frac {\partial U } {\partial V } \right) _{T} +P \right) } \left ( \frac {\partial V } {\partial T } \right) _{P} \right ] }$ ……….(1)$dQ = \left ( \frac {\partial U } {\partial T } \right) _{V} dT + \left ( \frac {\partial U } {\partial V } \right) _{T} dV + p dV$ …….(2)

In the above equation Q is a function of V and T.

$\left ( \frac {\partial Q } {\partial T } \right) _{V} = \left ( \frac {\partial U } {\partial T } \right) _{V} + 0 +0 = C_V$....(3)

The more correct formulation is:

Q itself is a physical quantity. Depending of the experiment, sometimes it could be a function of V and T or P and T i.e. whether Q is Q = Q(V,T) or Q = Q(P,T) depends upon the experiment.

When Q is a function of V and T i.e. Q = Q( V,T),

We have,

$\left ( \frac {\partial Q } {\partial T } \right) _{V} = \left ( \frac {\partial U } {\partial T } \right) _{V} + 0 +0 = C_V$....(3)

When Q is a function of P and T i.e. Q = Q( P,T),

We have,

$\left ( \frac {\partial Q } {\partial T } \right) _{P} = C_P= \left ( \frac {\partial U } {\partial T } \right) _{V} + \{ \left ( \frac {\partial U } {\partial V } \right) _{T} + p\} \left ( \frac {\partial V } {\partial T } \right) _{P}$ …….(4)

In equation 2 and 3, we have expressed both U and Q as a function of V and T.

In equation 4, we have expressed U as a function of V and T( so we have got equation 2), but we have expressed Q as a function of P and T.

Isn’t it always true that when U is a function of V and T, then Q must be a function of V and T or when Q is a function of P and T, then U must be a function of P and T?

In equation 4, we have expressed Q = Q (P,T), so the independent variables are P and T.

V is a function of P and T i.e. V = V(P,T), while U is a function of V and T i.e. U = U(V,T). Since here V is a function of P and T, U = U(V,T) = U(V(P,T), T) = U(P,T).

So, expressing U as a function of P and T,

We have,

$C_P = \left ( \frac {\partial Q } {\partial T } \right) _{P} = \left ( \frac {\partial U } {\partial T } \right) _{P} +P \left ( \frac {\partial V } {\partial T } \right) _{P}$

Then, we have to find $\left ( \frac {\partial U } {\partial T } \right) _{P}$ applying Maxwell relations upon G(P,T).

Is this correct?

I am very confused by what you have done here. Are you aware that, in irreversible processes, P, T, or even both P and T are non-uniform within the system. In that case, what value of P or T do you use? If you are calling Q the enthalpy, or is it the heat? If it is the heat, then, even for reversible processes between two thermodynamic equilibrium states, Q and W are not unique. So, you can't express Q as a function of the parameters P, V, and T at a thermodynamic equilibrium state (even if you did also include the parameters at the initial state).

 

[Pushoam]

As Q (heat)is not a state function, we cannot express it as a function of state variables.
But then doesn't the eqn.
$dQ = \left ( \frac {\partial U } {\partial T } \right) _{V} dT + \left ( \frac {\partial U } {\partial V } \right) _{T} dV + p dV$ tell that Q is a function of V and T?
$\left ( \frac {\partial Q } {\partial T } \right) _{V} =C_V$ means that Q is fn of V and T, dosn't it?
A partial differentiation is defined only for a well defined function. If Q is not a fn of V and T, then Q is a fn of which variables?
If Q is not a well - defined fn, then how do we calculate heat given to a system for a given process?

Actually, Q is well - defined. The point is : the value of Q is different for different process. Q is a process dependent fn or path dependent fn. So, when the path is given, Q is defined. For $\left ( \frac {\partial Q } {\partial T } \right) _{V} =C_V$ , the process is an isochoric process, and hence, for this process, Q is a function of T. Is this correct?

I myself am getting confused here. So sorry if it doesn't make sense what I am writing here. I will take another try. I may be then able to formulate better where I am stuck.

 

[Charles Link]

As Q (heat)is not a state function, we cannot express it as a function of state variables.
But then doesn't the eqn.
$dQ = \left ( \frac {\partial U } {\partial T } \right) _{V} dT + \left ( \frac {\partial U } {\partial V } \right) _{T} dV + p dV$ tell that Q is a function of V and T.
$\left ( \frac {\partial Q } {\partial T } \right) _{V} =C_V$ means that Q is fn of V and T.
A partial differentiation is defined only for a well defined function. If Q is not a fn of V and T, then Q is a fn of which variable?

I myself am getting confused here. So sorry if it doesn't make what I am writing here. I will take another try. I may be then able to formulate where I am stuck.

I think I can help answer this question: Generally $Q$ is not used in expressions like these. If it is a reversible process, then what is used in place of $dQ$ is $TdS$. The entropy $S$ is a state function. Wikipedia calls $Q$ and $W$ "process functions" as compared to the other quantities such as internal energy $U$, enthalpy $H$, and entropy $S$, which are "state functions".

 

[Pushoam]

I think I can help answer this question: Generally $Q$ is not used in expressions like these. If it is a reversible process, then what is used in place of $dQ$ is $TdS$. The entropy $S$ is a state function. Wikipedia calls $Q$ and $W$ "process functions" as compared to the other quantities such as internal energy $U$, enthalpy $H$, and entropy $S$, which are "state functions".

dQ = T dS for a reversible process.
Since both S and T are state - fn.,T dS is same for each path. Hence, the if we integrate TdS between the final and initial states, the integral i.e. Q also should be independent of the path. Does this mean that Q is a path - independent function for a reversible process?
But in thermodynamics, mostly, reversible processes are studied as each step of reversible process is in thermodynamic equillibrium and only in this eqbm, the state variables are well - defined.

 

[Charles Link]

dQ = T dS for a reversible process.
Since both S and T are state - fn.,T dS is same for each path. Hence, the if we integrate TdS between the final and initial states, the integral i.e. Q also should be independent of the path. Does this mean that Q is a path - independent function for a reversible process?
But in thermodynamics, mostly, reversible processes are studied as each step of reversible process is in thermodynamic equillibrium and only in this eqbm, the state variables are well - defined.

I think what you are saying is correct, but @Chestermiller is really the Thermodynamics expert. It takes a lot of practice to get proficient at working thermodynamic problems. The entropy $S$ is a very different concept that takes a while to become well-acquainted with it . $\\$ In a reversible process, at each step in the process, I believe there is equilibrium. You can pause a reversible process in the middle of the process=e.g. the reversible expansion of a gas, and the system will remain in that equilibrium state. And what you say is also correct, in irreversible processes, the state functions are not well defined, and not unique.

 

[Chestermiller]

As Q (heat)is not a state function, we cannot express it as a function of state variables.
But then doesn't the eqn.
$dQ = \left ( \frac {\partial U } {\partial T } \right) _{V} dT + \left ( \frac {\partial U } {\partial V } \right) _{T} dV + p dV$ tell that Q is a function of V and T?

This equation is not valid for an irreversible path. That is because, unless the path is reversible, the work is not pdV. Moreover, it is always a bad idea to write a thermodynamic equation in terms of differentials unless the path is reversible. Even then, this equation would be valid only for the change between two closely neighboring equilibrium states. Plus, if you took two different tortuous reversible paths between the same two closely neighboring equilibrium states, in general, the total Q and the total W could differ between paths; they would just be nearly equal to one another for each path.

$\left ( \frac {\partial Q } {\partial T } \right) _{V} =C_V$ means that Q is fn of V and T, dosn't it?

No. The correct relationship is $\left ( \frac {\partial U } {\partial T } \right) _{V} =C_V$. U is a unique function of V and T for equilibrium states, not Q.

A partial differentiation is defined only for a well defined function. If Q is not a fn of V and T, then Q is a fn of which variables?
If Q is not a well - defined fn, then how do we calculate heat given to a system for a given process?

Q is the amount of heat added from the surroundings to the system, irrespective of whether the process is reversible or irreversible? Check your textbook and see how Q is calculated for various processes. Sometimes it is specified in the problem statement, sometimes it is backed out of the first law (knowing the work and the change in internal energy), and sometimes it is determine from the change in the surroundings internal energy. It is never calculated from a change in V and T.

Actually, Q is well - defined. The point is : the value of Q is different for different process. Q is a process dependent fn or path dependent fn. So, when the path is given, Q is defined. For $\left ( \frac {\partial Q } {\partial T } \right) _{V} =C_V$ , the process is an isochoric process, and hence, for this process, Q is a function of T. Is this correct?

This is one of the cases in which is it backed out from the first law $\Delta U$.

 

[Chestermiller]

dQ = T dS for a reversible process.
Since both S and T are state - fn.,T dS is same for each path. Hence, the if we integrate TdS between the final and initial states, the integral i.e. Q also should be independent of the path. Does this mean that Q is a path - independent function for a reversible process?

This is not correct mathematically. We can create many Carnot cycles in which the temperatures at which heat transfer occurs are the same and the change in entropy is the same (zero), but for which the net heat transferred is not the same.

 

[Pushoam]

This equation is not valid for an irreversible path. That is because, unless the path is reversible, the work is not pdV.

The above equation comes from the 1st law of thermodynamics ( $\Delta U = \Delta Q + \Delta W$)which is valid for ( I think ) both reversible and irreversible processes.

For reversible process, U as a function of V and T and dW = - p dV are defined. So, the above equation is valid only for reversible process. Right ?

Even then, this equation would be valid only for the change between two closely neighboring equilibrium states.

Is this because the above eqn deals with the infinitesimal change and the difference between two closely neighboring eqbm states is infinitesimal?

$\left ( \frac {\partial Q } {\partial T } \right) _{V} =C_V$means that Q is fn of V and T, dosn't it?

No. The correct relationship is $\left ( \frac {\partial U } {\partial T } \right) _{V} =C_V$. U is a unique function of V and T for equilibrium states, not Q.

The book says,

Here, $C_V$ is defined as $C_V = \left ( \frac {\partial Q } {\partial T } \right) _{V}$ and then on calculation it is found that $C_V = \left ( \frac {\partial U } {\partial T } \right) _{V}$.

What I have understood from your statement as $C_V$ is defined as $C_V = \left ( \frac {\partial U } {\partial T } \right) _{V}$.
Is this correct?

Q is the amount of heat added from the surroundings to the system, irrespective of whether the process is reversible or irreversible? Check your textbook and see how Q is calculated for various processes. Sometimes it is specified in the problem statement, sometimes it is backed out of the first law (knowing the work and the change in internal energy), and sometimes it is determine from the change in the surroundings internal energy. It is never calculated from a change in V and T.

For any reversible process,

$\Delta U$ between any two states or dU between any two close states is well defined independently of path.

$\Delta Q$ between any two states or dQ between any two close states is well defined for any given path.

So, U is well defined as a function of state variables independently of the path.

And Q is well defined as a function of the state variables for a given path. Isn’t it so?

The book says that for reversible process both TdS and pdV are differrential of state fn. So, their definite integral i.e Q and W respectively should also be state fn. But, it is said that Q and W are not state fn. This is where I am stuck.

 

[Chestermiller]

View attachment 214876
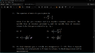
The above equation comes from the 1st law of thermodynamics ( $\Delta U = \Delta Q + \Delta W$)which is valid for ( I think ) both reversible and irreversible processes.

For reversible process, U as a function of V and T and dW = - p dV are defined. So, the above equation is valid only for reversible process. Right ?

For an irreversible path, p and T are not uniform within the system, and viscous stresses contribute to the force per unit area that the gas exerts on the surroundings, so the equation of state can not be used to establish the force on the surroundings or the work. Also, for both an irreversible path or a reversible path, the "volumetric" work done by the system on the surroundings can be determined by integrating $p_{ext}dV$, where $p_{ext}$ is the force per unit area exerted by the surroundings on the system (if this force is somehow known or specified). In the case of a reversible path, $p_{ext}$ also matches the pressure of the gas within the system p calculated from the equation of state.

Is this because the above eqn deals with the infinitesimal change and the difference between two closely neighboring eqbm states is infinitesimal?

Yes.

The book says,
View attachment 214876

Here, $C_V$ is defined as $C_V = \left ( \frac {\partial Q } {\partial T } \right) _{V}$ and then on calculation it is found that $C_V = \left ( \frac {\partial U } {\partial T } \right) _{V}$.

What I have understood from your statement as $C_V$ is defined as $C_V = \left ( \frac {\partial U } {\partial T } \right) _{V}$.
Is this correct?

I completely disagree with how this is presented in your book, and, as justification for this disagreement, I cite your present state of confusion.

In freshman physics, they taught us that $Q=C\Delta T$, where they called C the heat capacity of the material and Q the heat transferred to the material. All the problems to which this was applied were ones in which no work was done.

Now we arrive at thermodynamics, and we encounter situations where work can be done on the surroundings. And immediately we encounter problems with using this old definition because Q is supposed to be (exclusively) the heat transferred from the surroundings to the system, while C is supposed to be a physical property of the material. And, when work is being done, Q is not longer equal to $C\Delta T$. So, in thermodynamics, we find it necessary to discard the old definition of C in terms of Q, and adopt a new definition in which we consistently get the right answer, whether or not work is being done, while, at the same time reducing to the old definition when work is not being done. This new definition is:
$$C_v=\left(\frac{\partial U}{\partial T}\right)_V$$and $$C_p=\left(\frac{\partial H}{\partial T}\right)_P$$These new definitions clear up all the difficulties with Q being energy in transit (specifically for a process) while C is a physical property of the material (independent of any process).

For any reversible process,

$\Delta U$ between any two states or dU between any two close states is well defined independently of path.

$\Delta Q$ between any two states or dQ between any two close states is well defined for any given path.

There are an infinite number of $\Delta Q$s or dQs between any two close states for the infinite number of paths between the two states. But there is only one $\Delta U$ or dU. So, clearly, Q is not a unique function of state. It is a function only of path. And the path cannot be specified giving the system temperature and pressure as a function of time along the path, because these are not uniform within the system for an irreversible path.

So, U is well defined as a function of state variables independently of the path.

Yes.

And Q is well defined as a function of the state variables for a given path. Isn’t it so?

No.

View attachment 214880
The book says that for reversible process both TdS and pdV are differrential of state fn. So, their definite integral i.e Q and W respectively should also be state fn. But, it is said that Q and W are not state fn. This is where I am stuck.

Q is not the definite integral of TdS and W is not the definite integral of PdV. This is only true for a reversible path. For an irreversible process, we can only know T at the boundary of the system (typically an ideal reservoir temperature, $T_R$), and, for such a process, the most that we can say is that $$\int{\frac{dQ}{T_R}}\lt\Delta S$$where $\Delta S$ is the change in entropy between the initial and final thermodynamic equilibrium states of the system (i.e., assuming that the final state is an equilibrium state). And, for both reversible and irreversible processes, $$W=\int{p_{ext}dV}$$.

Here is an article I wrote for Physics Forums Insights that I wrote a couple of years ago that might help: https://www.physicsforums.com/insights/understanding-entropy-2nd-law-thermodynamics/