Bashyboy
- 1,419
- 5
Homework Statement
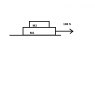
In the figure, a slab of mass m1=40kg rests on a frictionless floor, and a block of mass m2=10kg
rests on top of the slab. Between block and slab, the coefficient of static friction is μs=0.60, and
the coefficient of kinetic friction is μk=0.40. A horizontal force F of magnitude 100 N begins to
pull directly on the block, as shown.
Homework Equations
The Attempt at a Solution
One question I have is, what sort of friction is acting, kinetic or static? I figured that it would be static. When the force F begins pulling on m1, intertia will act to keep m2 from sliding with the slab, giving it the impression that it is moving to the left, relative to the slab's point of view. Hence, the static friction force will balance this "inertial force" that is trying to act, thereby causing the block to move in unison with the slab, or mathematically, a1 = a2.
How do I prove this mathematically, though. Do I need to compute the static friction force and compare it to some other force?