Studiot said:
I understand and agree with it, with one proviso: It is not a source of bouyancy, indeed it will act in addition to any bouyancy force.
It is an upward force... It is caused by water displacement... The force is essentially equal to the weight of the water that would have filled the cylinder (assuming a lightweight cylinder)... Does any reference define this phenomenon as anything other than buoyancy? If so, I'd like to look at it; I'm not excluding the possibility that I'm wrong.
Studiot said:
But the reaction force between the base and the support block must equal the weight of the support plus whatever it is supporting. So all your gauge is measuring is the weight of the second box as I said before.
For simplicity, I was ignoring the weight of the empty cylinder compared to the weight of the water that it displaced. But yes, to be
super precise, the stress state in the support is
\left[\begin{array}{ccc}<br />
-\rho g h(1-\frac{z}{h}) & 0 & 0\\<br />
0 & -\rho g h(1-\frac{z}{h}) & 0\\<br />
0 & 0 & -\rho g (h-t_\mathrm{supp})-\frac{W_\mathrm{supp}}{A}(1-\frac{z}{t_\mathrm{supp}})<br />
\end{array}\right]
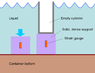
in the first case (left side of the diagram) and
\left[\begin{array}{ccc}<br />
-\rho g h(1-\frac{z}{h}) & 0 & 0\\<br />
0 & -\rho g h(1-\frac{z}{h}) & 0\\<br />
0 & 0 & -\frac{W_\mathrm{cyl}}{A}-\frac{W_\mathrm{supp}}{A}(1-\frac{z}{t_\mathrm{supp}})<br />
\end{array}\right]
in the second case (right side of the diagram), where \rho is the water density, g is gravitational acceleration, h is the depth to the container floor, W_\mathrm{supp} and t_\mathrm{supp} are the weight and height of the support, respectively, A is the cross-sectional area of the cylinder and support, z is the vertical distance from the container floor, and W_\mathrm{cyl} is the weight of the empty cylinder.
I believe it has been assumed in this entire thread that the empty cylinder weighs less than an equal volume of water.
The attachment of the empty cylinder thus corresponds to the
addition of a normal
tensile stress \rho g(h-t_\mathrm{supp})-W_\mathrm{cyl}/A in the vertical direction. This is buoyancy.
EDIT: Whoops, should have been \rho g(h-t_\mathrm{supp}) instead of \rho g h.