skatenerd said:
In the middle of an integral using Green's Theorem for an outward flux calculation, I came up to a really gross integral. The double integral started out as
$$\int_{-1}^{1}\int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}\frac{2}{1+y^2}\,dx\,dy$$
and I got it down to
$$\int_{-1}^{1}\frac{4\sqrt{1-y^2}}{1+y^2}\,dy$$
I tried thinking of numerous substitutions and by parts strategies...nothing seemed to work. I consulted wolframalpha and it gave me a solution using I think something like 4 substitutions and partial fractions which I would really rather not go through.
Any other ideas? Or is this just a terrible integral one would prefer to avoid?
I can't think of an easy way to do this one. I think converting to polar coordinates may ease the pain at the start, but from what you'll see below, it's still quite a messy process.
If you plot the region that's defined by the bounds of integration, it's a circle of radius 1 centered at the origin in the $xy$-plane.
If you do the conversion to polar coordinates, we see that
\[\int_{-1}^1\int_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}} \frac{2}{1+y^2}\,dx\,dy \xrightarrow{\text{polar coordinates}}{} \int_0^{2\pi} \int_0^1\frac{2r}{1+ r^2\sin^2\theta}\,dr\,d\theta\]
The first intergral can be evaluated by making the substitution $u=r^2\sin^2\theta$; then $\,du=2r\sin^2\theta\,dr\implies \dfrac{\,du}{\sin^2\theta}=2r\,dr$. Thus,
\[\int_0^{2\pi} \int_0^1\frac{2r}{1+r^2\sin^2\theta}\,dr\,d\theta \xrightarrow{u=r^2\sin^2\theta}{} \int_0^{2\pi}\int_0^{\sin^2\theta} \frac{1}{\sin^2\theta} \frac{\,du}{1+u}\,d\theta = \int_0^{2\pi} \frac{\ln(1+\sin^2\theta)}{\sin^2\theta} \,d\theta\]
Now here's where all the fun begins.
We proceed to integrate by parts (w/o limits of integration for the time being). Take $u=\log(1+\sin^2\theta)$ and $\,dv=\dfrac{\,d\theta}{\sin^2\theta}=\csc^2\theta\,d\theta$. Then $\,du=\dfrac{2\sin\theta\cos\theta}{1+\sin^2\theta}\,d\theta$ and $v=-\cot\theta$. Therefore,
\[\begin{aligned}\int \frac{\ln(1+\sin^2\theta)}{\sin^2\theta}\,d\theta &= -\cot\theta\ln(1+\sin^2\theta) + \int \frac{2\cot\theta\sin\theta\cos\theta}{ 1+\sin^2\theta}\,d\theta\\ &= -\cot\theta\ln(1+\sin^2\theta) +\int\frac{2\cos^2\theta}{1+\sin^2\theta}\,d\theta\end{aligned}\]
Now, to integrate $\displaystyle\int\frac{2\cos^2\theta}{ 1+\sin^2\theta}\,d\theta$, multiply top and bottom by $\sec^4\theta$ to get
\[\int\frac{2\sec^2\theta}{\sec^4\theta + \sec^2\theta\tan^2\theta}\,d\theta = \int\frac{2\sec^2\theta}{(\tan^2\theta+1)^2 + (\tan^2+ 1)\tan^2\theta}\,d\theta = \int\frac{2\sec^2\theta}{2\tan^4\theta +3\tan^2\theta + 1}\,d\theta\]
Now let $t=\tan\theta\implies \,dt=\sec^2\theta\,d\theta$. Therefore,
\[\int\frac{2\sec^2\theta}{2\tan^4\theta +3\tan^2\theta + 1}\,d\theta \xrightarrow{t=\tan\theta}{} \int\frac{2\,dt}{2t^4+3t^2+1} = \int\frac{2\,dt}{(2t^2+1)(t^2+1)}\]
If things aren't bad enough at this point, things just got worse; it's time to use partial fractions! XD
We first note that
\begin{align*}\frac{1}{(2t^2+1)(t^2+1)}=\dfrac{At+B}{2t^2+1} +\dfrac{Ct+D}{t^2+1} \implies 1 &= (At+B)(t^2+1) + (Ct+D)(2t^2+1) \\ \implies 1 &= At^3+Bt^2+At+B + 2Ct^3+2Dt^2+Ct+D\\ \implies 1 & = (A+2C)t^3+(B+2D)t^2 + (A+C)t + (B+D)\end{align*}
Thus, we solve the system of equations
\[\left\{\begin{aligned}A+2C &= 0\\ B+2D &= 0\\ A+C &= 0\\ B+D &= 1 \end{aligned}\right.\]
It's easy to show that $A=C=0$, $D=-1$ and $B=2$.
Therefore, \[\begin{aligned} \int\frac{2}{(2t^2+1)(t^2+1)}\,dt &= 2\left[\int\frac{2}{2t^2+1}\,dt - \int\frac{1}{t^2+1}\,dt\right]\\ &= 2\left[\sqrt{2}\int\frac{\sqrt{2}}{(\sqrt{2}t)^2+1}\,dt - \int\frac{1}{t^2+1}\,dt\right]\\ &= 2\left[\sqrt{2}\arctan(\sqrt{2}t) - \arctan(t)\right]+C\end{aligned}\]
Since $t=\tan\theta$, we have that
\[2\left[\sqrt{2}\arctan(\sqrt{2}\tan\theta) - \arctan(\tan\theta)\right]+C = 2\sqrt{2}\arctan(\sqrt{2}\sin\theta) -2\theta+C\]
and thus
\[\int\frac{2\cos^2\theta}{1+\sin^2\theta}\,d\theta = 2\sqrt{2}\arctan(\sqrt{2}\tan\theta) - 2\theta + C\]
and furthermore we now have that
\[\int \frac{\ln(1+\sin^2\theta)}{\sin^2\theta}\,d\theta = -\cot\theta\ln(1+\sin^2\theta) + 2\sqrt{2}\arctan(\sqrt{2}\tan\theta) -2\theta+C\]
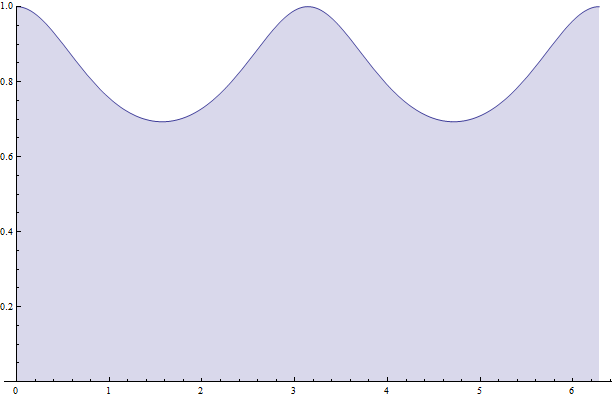
We must take note of something due to the oscillatory nature of $\dfrac{\ln(1+\sin^2\theta)}{\sin^2\theta}$ seen below over the interval $[0,2\pi]$:
If we were to evaluate the integral over $[0,2\pi]$, lots of things would be ignored and we end up with an answer of $-4\pi$ (which makes no sense). From the graph, it makes sense to evaluate the integral from $[0,\pi/2]$ and then multiply that result by 4 to get the entire area. With that said, it follows now that
\[\begin{aligned} \int_0^{2\pi} \frac{\ln(1+\sin^2\theta)}{\sin^2\theta}\,d\theta &= 4\int_0^{\frac{\pi}{2}} \frac{\ln(1+\sin^2\theta)}{\sin^2\theta}\,d\theta \\ &= 4\left[-\cot\theta\ln(1+\sin^2\theta) + 2\sqrt{2}\arctan(\sqrt{2}\tan\theta) -2\theta\right]_0^{\frac{\pi}{2}} \\ &= 4\left[ \left( -\cot\frac{\pi}{2} \ln\left(1+\sin^2\frac{\pi}{2}\right) + \lim_{b\to\frac{\pi}{2}^-} 2\sqrt{2} \arctan\left(\sqrt{2}\tan b\right) -\pi\right)\right.\\ & \phantom{=.4.} \left.-\left( \lim_{a\to 0^+} -\cot a\ln(1+\sin^2 a) +2\sqrt{2} \arctan(\sqrt{2} \tan 0) \right)\right] \\ &= 4\left[(\sqrt{2}\pi -\pi) - \underbrace{\lim_{a\to 0^+} -\cot a\ln(1+\sin^2 a)}_{=0\text{ by L'Hôpital's rule}}\right]\\ &= 4\pi(\sqrt{2}-1)\approx 5.20516\end{aligned}\]
Which luckily matches up with the numerical value provided by WolframAlpha (!)
(Whew)
It's a lot to read through, but I hope this makes sense! XD
EDIT: Ninja'd by chisigma by about an hour or so... >_>