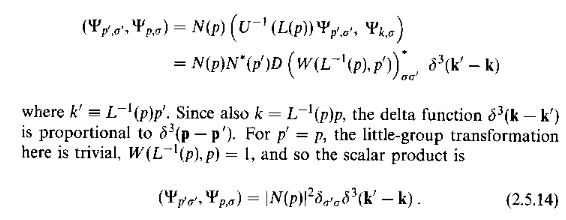Is this a mistake in Weinberg's book?

[kent davidge]

The image is below. My question is, why he considers $p' = p$ on the RHS of $(2.5.14)$ but not on the LHS, i.e., the sub index on the left $\Psi$ remains $p'$. Is it a mistake? And he continues on the derivation (not shown here) even considering $|N(p)|^2$ instead of $N(p')^*N(p)$ so it doesn't seem like a typo.

 

[Demystifier]

Because $f(p,p')\delta(p-p')=f(p,p)\delta(p-p')$ for any "well behaved" function $f(p,p')$.

 

[kent davidge]

Sounds a little tough that Weinberg supposes we knew that before reading the text.

That's not what I would expect from a serious author

 

[George Jones]

Sounds a little tough that Weinberg supposes we knew that before reading the text.

But this is what a delta function does.

That's not what I would expect from a serious author

Sorry, but I think that this is both untrue and unfair. This is something that I would expect from a serious author of a graduate-level textbook.

 

[PeterDonis]

That's not what I would expect from a serious author

As @George Jones points out, Weinberg's text is a graduate level text. That corresponds to an "A" level thread here at PF. The basic properties of delta functions are indeed part of the background someone would be expected to have for an "A" level discussion here. You labeled this thread as "I", indicating undergraduate level, so it's understandable that you might not have that background; but that just means you are not really the intended audience of Weinberg's text. (Not that that's a problem; taking on a text at a higher level can be a good learning experience. But you should expect to come up against instances like this where the text assumes background knowledge that you don't have, because the text is aimed at a more advanced audience.)

 

[vanhees71]

Sounds a little tough that Weinberg supposes we knew that before reading the text.

That's not what I would expect from a serious author

Ehm, well, if you start with relativistic QFT you should indeed know fundamental facts about distributions. In physics you almost always only need Dirac's $\delta$ distribution, which is treated on the relevant level in any good textbook on theoretical classical electrodynamics, a subject taught in the 3rd-semester theory-course lecture.

That said, Weinberg is a very advanced textbook, treating many details of QFT in the most general sense (e.g., particles for arbitrary spin). That's why it's unlikely that you understand the subject using it as your first book on QFT. For that purpose, I recommend

M. D. Schwartz, Quantum Field Theory and the Standard Model, Cambridge University Press

Then you can appreciate Weinberg to learn some more subtle details, particularly from a very "practical" point of view, "why QFT is the way it is" (answer: Poincare symmetries+causality). To learn other more subtle details you should also consider the excellent book

A. Duncan, The Conceptual Framework of Quantum Field Theory, Oxford University Press

which has of course a lot of overlap with Weinberg but also treats subjects not found in Weinberg, like "How to stop worrying about Haag's theorem" and some other puzzles of this kind, you always encounter when involved with QFT, which is an addictive subject anyway :-)).

 

[kent davidge]

Thank you all for your opinions/replies/advice.