JC2000
- 186
- 16
- Homework Statement
- Show that :
$$
\beta(p, q)=\int_{0}^{\infty} \frac{y^{q-1}}{(1+y)^{p+q}} d y
$$
- Relevant Equations
- The Beta Function :
$$
\beta(m, n)=\int_{0}^{1} x^{m-1}(1-x)^{n-1} d x
$$
The solution is as follows :
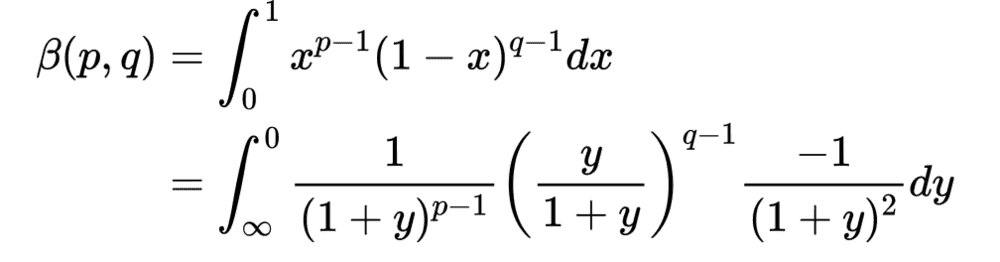
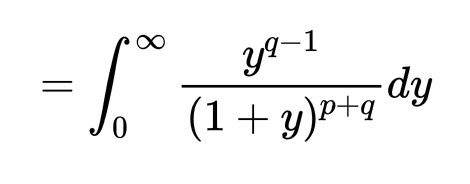 The substitution is what nags me , which is as follows :
The substitution is what nags me , which is as follows :
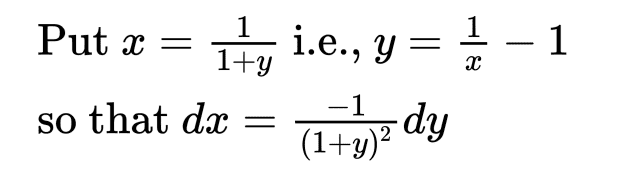
This substitution "trick" to me seems impossibly difficult to arrive at "logically" without pretty much reverse engineering the problem.
So is this simply a lack of practice/ familiarisation showing ? I feel like I have always struggled with similar manipulations. In the past I think it was through repeatedly encountering a certain peculiar manipulation that it would become second nature for me. Is this how such problems are to be approached? Since it seems to almost be the same as memorising the solution!
Thank you for your insight!
This substitution "trick" to me seems impossibly difficult to arrive at "logically" without pretty much reverse engineering the problem.
So is this simply a lack of practice/ familiarisation showing ? I feel like I have always struggled with similar manipulations. In the past I think it was through repeatedly encountering a certain peculiar manipulation that it would become second nature for me. Is this how such problems are to be approached? Since it seems to almost be the same as memorising the solution!
Thank you for your insight!