Born
- 31
- 1
Homework Statement
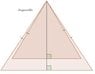
Problem 99 from "Kiselev's Geometry Book I - Planimetry":
Two isosceles triangles with a common vertex and congruent lateral sides cannot fit one inside the other.
Homework Equations
The Attempt at a Solution
The statement is obviously true. If we visualize each isosceles triangle as made from two right triangles then we see that in order for one to fit in the other both the base and the height of one should be smaller than the bade and height of the other, however this is not possible since the sides of the smaller right triangle would not be able to connect to the endpoints of the hypotenuse by the Pythagorean theorem.
Sadly, the Pythagorean theorem comes later in the book. All I have are some more simple theorems, such as "the greater angle opposes the greater side" and "the greatest slant drawn from a point to a line is the one with the greatest distance from the foot of the perpendicular of the line to the point".
Any help is welcome