Isothermal and adiabatic air compression -- different expressions

[Ameen1985]

Hi all,
For an Isothermal compression process of air in a vessel with constant volume, I found the following expressions

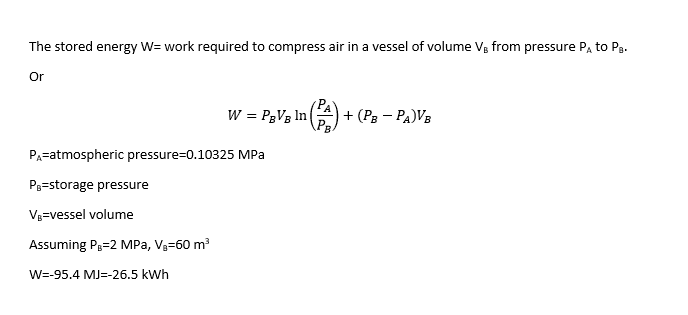
and

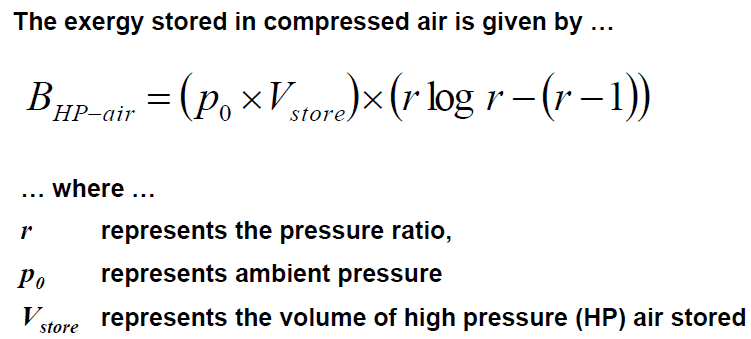
and

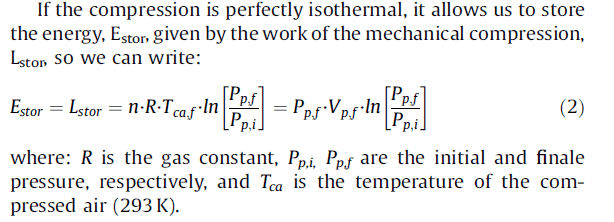
The first two give the same result, meanwhile the third gives another solution and I don't know why.

For adiabatic compression I found these two expression which also give different answers. Can someone please help me with this.

and

Let's say we have a 11 kWh to be stored in compressed air, P0 = 101325 Pa, P1 = 6.3 bar, P2 = 10 bar, and T0= 298 K. What would be the required air vessel volume?

 

[Chestermiller]

It isn't clear what the processes are that are involved here. Can you please describe them.

 

[Ameen1985]

It isn't clear what the processes are that are involved here. Can you please describe them.

The first three expressions should be Isothermal compression. However, The first 2 give the same answer and the third equation not.

The other two expressions should be used for adiabatic compression but both give me different answers with big difference
I don't know why.

 

[Chestermiller]

The first three expressions should be Isothermal compression. However, The first 2 give the same answer and the third equation not.

The other two expressions should be used for adiabatic compression but both give me different answers with big difference
I don't know why.

I wasn't asking for a 2-word description. I was asking for a detailed description, something along the lines of "I have a compressor that takes air at atmospheric pressure and compresses it to PB while being connected through an open valve to a tank of volume V initially at atmospheric pressure. The final pressure in the tank is PB. The process is done either adiabatically or isothermally," if this is what the process actually is. It is hard to see from your equations what the actual process was.

 

[Ameen1985]

I wasn't asking for a 2-word description. I was asking for a detailed description, something along the lines of "I have a compressor that takes air at atmospheric pressure and compresses it to PB while being connected through an open valve to a tank of volume V initially at atmospheric pressure. The final pressure in the tank is PB. The process is done either adiabatically or isothermally," if this is what the process actually is. It is hard to see from your equations what the actual process was.

Sorry for my previous reply.
In my original post, I wrote that I have 11 kWh to be stored in compressed air and I want to know the required tank volume.
The compressed air will be used to run an air motor at 6.3 bar. Therefore, the minimum air pressure inside the tank should be 6.3 bar (Pm or P1 = 6.3 bar as described in the 4th and 5th expressions)
The maximum air tank pressure is 10 bar (P2 = 10 bar) and of course P0 = 1 bar and T0= 298 K. What would be the required air vessel volume?

 

[Chestermiller]

Is the system below anything like what you are interested in:

 

[anorlunda]

In his other thread, he posted this after some prodding (and assumed that anyone who read this thread also read the other):

 

[Chestermiller]

There is actually a very close connection between the problem I presented in post #6, and Eqns. 1 and 2 in the section headed 2.1 Compressor... in your writeup.

The process being considered in section 2.1 involves an adiabatic tank of volume $V_1$ that is being filled by a continuously operating adiabatic compressor. The air entering the compressor and the air within the tank are both initially at atmospheric temperature $T_0$. The initial pressure of the air in the tank is $P_1>P_0$ and the pressure of the air at the entrance to the compressor is $P_0$, atmospheric. Throughout the process, the air pressure exiting the compressor is constant at $P_2>P_1$. During the process, the air from the compressor passes through a valve in which its pressure drops from $P_2$ to whatever pressure P is present within the tank at that moment in time. Eventually, the pressure P in the tank rises to the value $P_2$ equal to the pressure of the air delivered by the compressor. At that point in time, the valve is closed and the filling process ends.

Eqn. 2 describes the temperature within the tank when the pressure reaches $P_2$. Eqn. 1 describes the total work done by the compressor during this filling operation.

 

[Ameen1985]

Many thanks @Chestermiller for your replys.
As @anorlunda mentioned, I consider the system shown in post #7.

My question is simple.
When I have 39600000 J (11 kWh) energy used to compress air where the minimum pressure is 630000 pa (6.3 bar) and the maximum pressure 1000000 pa (10 bar) and pressure ratio = (10/6.3).

The first and second equations in my post gives the same 430.3 m3 required tank volume while the 3 equation give a 86 m3 ! the 3 equations should represent isothermal compression. What is the cause of this ??

My second part of the question about adiabatic compression which should be presented by equation 4 and 5 in my original post.
When I use the same inputs of compression energy 39600000 J, K= n = 1.4, P0=101325, T0=298 K, P0 (pressure outside the vessel) = 101325, minimum pressure = 630000, maximum Pressure = 1000000 pascal. The required volume = 50 m3 and 46 m3 using equations 4 and 5. Why this difference ?

 

[Chestermiller]

Please bring me up to speed. How is the system in post #7 supposed to be operated? I don't want any numbers. It's supposed to be a temporary energy storage facility by somehow running the compressor during peak times and transferring some of the energy via heat to the water. Then, later it is recovered from the water and input to the air to run a generator. Please provide qualitative details on the operating procedure for such a system.

 

[Ameen1985]

Please bring me up to speed. How is the system in post #7 supposed to be operated? I don't want any numbers. It's supposed to be a temporary energy storage facility by somehow running the compressor during peak times and transferring some of the energy via heat to the water. Then, later it is recovered from the water and input to the air to run a generator. Please provide qualitative details on the operating procedure for such a system.

As you mentioned, extra electricity from the PV plant will run the compressor to compress air to the receiver to be used offpeak. The heat generated during compression will be saved in the hot water tank to be used during air expansion in the air motor. Cold water from the air expansion will be used to cool the air during compression.

 

[Chestermiller]

This is an analysis of the isothermal compression problem, using a steady-flow compressor in which the mass holdup within the compressor is negligible compared to holdup in the tank volume V.

Let n = number of moles of air in tank at time t
$n_0=$ number of moles of air in tank at time zero
P = pressure in tank at time t
$P_0=$ pressure in tank at time zero = atmospheric pressure = pressure at inlet to compressor at all times

Then, for isothermal tank operation, we have $$P=P_0\frac{n}{n_0}$$We assume that the outlet pressure from the compressor is equal to the air temperature within the tank at all times. Here is the analysis of the steady flow compressor operation: From the open system (control volume) version of the first law of thermodynamics, we have $$\frac{dW_S}{dt}=\frac{dQ}{dt}$$where $W_S$ is the shaft work done by the compressor on the surroundings and Q is the heat added to the compressor. From the open system (control volume) version of the 2nd law of thermodynamics, for essentially reversible operation of the compressor, we have $$\frac{1}{T}\frac{dQ}{dt}=(\Delta s)\frac{dm}{dt}$$where $\Delta s=-R\ln{(P/P_0)}$ is the change in entropy per unit mass of air passing reversibly through the isothermal compressor at temperature T, and $\frac{dm}{dt}$ is the air molar flow rate through the compressor: $$\frac{dm}{dt}=\frac{dn}{dt}$$
If we combine the previous equations, we obtain:
$$\frac{dW_s}{dt}=-\frac{n_0}{P_0}RT\ln{(P/P_0)}\frac{dP}{dt}=-V\ln{(P/P_0)}\frac{dP}{dt}$$
If we integrate this equation from time t = 0 (where $P=P_0$) to arbitrary time t, we obtain: $$W_S=-P_0V[r\ln{r}-(r-1)]$$where $$r=\frac{P}{P_0}$$Physically, $W_S$ is the shaft work done by the compressor on the surroundings. So, for compressing the air into the tank, $W_S$ is minus the work to compress the air.

Because this is a steady flow system, the work done differs from that for a single-stroke closed system compressor.

 

[Ameen1985]

This is an analysis of the isothermal compression problem, using a steady-flow compressor in which the mass holdup within the compressor is negligible compared to holdup in the tank volume V.

Let n = number of moles of air in tank at time t
$n_0=$ number of moles of air in tank at time zero
P = pressure in tank at time t
$P_0=$ pressure in tank at time zero = atmospheric pressure = pressure at inlet to compressor at all times

Then, for isothermal tank operation, we have $$P=P_0\frac{n}{n_0}$$We assume that the outlet pressure from the compressor is equal to the air temperature within the tank at all times. Here is the analysis of the steady flow compressor operation: From the open system (control volume) version of the first law of thermodynamics, we have $$\frac{dW_S}{dt}=\frac{dQ}{dt}$$where $W_S$ is the shaft work done by the compressor on the surroundings and Q is the heat added to the compressor. From the open system (control volume) version of the 2nd law of thermodynamics, for essentially reversible operation of the compressor, we have $$\frac{1}{T}\frac{dQ}{dt}=(\Delta s)\frac{dm}{dt}$$where $\Delta s=-R\ln{(P/P_0)}$ is the change in entropy per unit mass of air passing reversibly through the isothermal compressor at temperature T, and $\frac{dm}{dt}$ is the air molar flow rate through the compressor: $$\frac{dm}{dt}=\frac{dn}{dt}$$
If we combine the previous equations, we obtain:
$$\frac{dW_s}{dt}=-\frac{n_0}{P_0}RT\ln{(P/P_0)}\frac{dP}{dt}=-V\ln{(P/P_0)}\frac{dP}{dt}$$
If we integrate this equation from time t = 0 (where $P=P_0$) to arbitrary time t, we obtain: $$W_S=-P_0V[r\ln{r}-(r-1)]$$where $$r=\frac{P}{P_0}$$Physically, $W_S$ is the shaft work done by the compressor on the surroundings. So, for compressing the air into the tank, $W_S$ is minus the work to compress the air.

Because this is a steady flow system, the work done differs from that for a single-stroke closed system compressor.

Many thanks @Chestermiller

 

[Chestermiller]

The first two equations given in your post #1 for an adiabatic compressor and tank assume that the pressure coming out of the compressor is always equal to the final pressure that will be present within the tank at the end of the process, while the pressure in the tank during the process gradually builds up to this final value. To operate in this way, there will be a throttle valve between the compressor and tank to drop the pressure from that emerging from the compressor and the current pressure within the tank. This type of compression results in a dissipation of mechanical energy and a lowering of efficiency.

On the other hand, the analysis in post #12 for an isothermal compressor and tank assumes that the instantaneous pressure coming out of the compressor is essentially equal to the current pressure within the tank at all times during the process. So the pressure within the tank and the exit pressure from the compressor build up gradually during the process, and there is no throttling with accompanying loss of efficiency and dissipation of mechanical energy. It is possible to analyze the adiabatic operation under this same mode of operation, which I will now do.

The application of the open system version of the first law of thermodynamics to the tank-filling goes as follows: $$\frac{d(un)}{dt}=h_{in}\frac{dn}{dt}\tag{1}$$where u is the specific internal energy of the gas within at time t, n is the number of moles of gas within the tank at time t, and $h_{in}$ is the specific enthalpy of gas exiting the compressor and entering the tank. With no loss of generality, we can write for an ideal gas $u=C_vT$ and $h_{in}=C_pT_{in}$. So Eqn. 1 becomes: $$C_v\frac{d(nT)}{dt}=C_pT_{in}dn\tag{2}$$It follows from the ideal gas law that $nT=\frac{PV}{R}$ and, from an analysis of the compressor adiabatic reversible operation that $T_{in}=T_0\left(\frac{P}{P_0}\right)^{\frac{\gamma-1}{\gamma}}$, where $T_0$ is the initial temperature of the air in the tank (before the process begins) and the temperature of the atmospheric air entering the compressor, and $P_0$ is the initial pressure of the air in the tank and the atmospheric pressure of the air entering the compressor, with $\gamma=C_p/C_v$ and V the (fixed) volume of the tank. If we substitute these relationships into Eqn. 2, we obtain:$$\frac{V}{R}\frac{dP}{dt}=\gamma T_0\left(\frac{P}{P_0}\right)^{\frac{\gamma-1}{\gamma}}\frac{dn}{dt}\tag(3)$$or, applying the ideal gas law to the tank contents at time zero, $$n_0\frac{d(P/P_0)}{dt}=\gamma\left(\frac{P}{P_0}\right)^{\frac{\gamma-1}{\gamma}}\frac{dn}{dt}\tag{4}$$Integrating this equation between time t = 0 and arbitrary time t, subject to the initial conditions $P=P_0$ and $n=n_0$ at time zero, yield the simple result that: $$\frac{n}{n_0}=\left(\frac{P}{P_0}\right)^{\frac{1}{\gamma}}\tag{5}$$This equation indicates that the air within the tank at any time during the operation has experienced the exact same adiabatic reversible compression as the air exiting the compressor has experienced at that same moment in time. In addition it means that not only is the air pressure exiting the compressor equal to the air pressure within the tank at all times, but so also is the air temperature exiting the compressor equal to the air temperature within the tank at all times.

The shaft work that the compressor does on the surroundings per mole of air passing through the compressor at time t is given by $-C_p(T-T_0)=-C_pT_0\left[\left(\frac{P}{P_0}\right)^{\frac{\gamma-1}{\gamma}}-1\right]$. Therefore, substituting Eqn. 5, the rate at which the compressor does shaft work on the surroundings is $$\frac{dW_S}{dt}=-C_pT_0\left[\left(\frac{P}{P_0}\right)^{\frac{\gamma-1}{\gamma}}-1\right]\frac{dn}{dt}$$$$=-\frac{C_pn_0T_0}{\gamma}\left[1-\left(\frac{P}{P_0}\right)^{-\frac{(\gamma-1)}{\gamma}}\right]\frac{d(P/P_0)}{dt}$$
This integrates to: $$W_S=C_pn_0T_0\left[\left(\frac{P}{P_0}\right)^{\frac{1}{\gamma}}-1-\frac{(P/P_0)-1}{\gamma}\right]$$$$=\frac{\gamma}{\gamma-1}P_0V\left[\left(\frac{P}{P_0}\right)^{\frac{1}{\gamma}}-1-\frac{(P/P_0)-1}{\gamma}\right]\tag{6}$$

This is the work done by the air on the shaft, and is minus the work done by the shaft to compress the air.

It is possible to show that Eqn. 6 applies not only to adiabatic reversible operation of the compressor and tank but also to any polytropic operation of this system, provided only that replace the isentropic index $\gamma$ with the polytropic index n. Furthermore, if we then take the limit of the expression as n approaches 1.0, we obtain the solution for isothermal operation of the system derived in the post # 12.