- #1
fightboy
- 25
- 0
Ok so for this example you have to calculate the net torque about an axis that passes through the hinges in each of the following cases in the image:
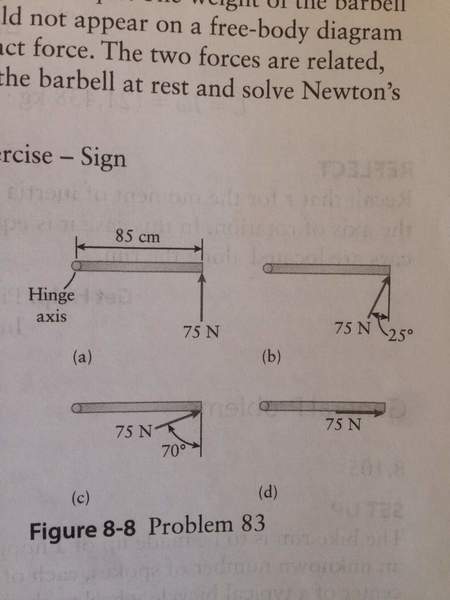
a) and c) were fairly straightforward to calculate but i had issues with b) and c). The solution listed the angle for b) as sin(115°) and for c) as sin(160°). I'm confused on where the 115° and 160° came from when the picture showed the angles as 25° and 70° respectively. Am I missing something? Thanks!
a) and c) were fairly straightforward to calculate but i had issues with b) and c). The solution listed the angle for b) as sin(115°) and for c) as sin(160°). I'm confused on where the 115° and 160° came from when the picture showed the angles as 25° and 70° respectively. Am I missing something? Thanks!