Joystick Geometry: Making a User Control for Opacities

[DaveC426913]

This is a programming issue, but the question is really about geometry. Let me 'splain.

I am making a page control in HTML/CSS/JS *no wait - come back! I swear it's not about programming!* that allows the user to play with the opacities of three overlapping images (eg. imageA = opacity 60, imageB=39, imageC opacity=1 ). The final 3 values must always sum to 100 (i.e. you cannot have 33,33,0). This means the space for the user to play in is not a simple 3D cube with full freedom along all 3 axes (such as many RGB controls have).

So the user can freely play with the "joystick" control by moving their mouse through the space. Note that what the user does, and what the values do - do not have be the exact same "space", as long as the user can manipulate the numbers intuitively.

My first solution is an equilateral triangle. No matter where they place the pointer in the triangle, we can measure the distance from each of the three apexes (or, to flip it over, we can measure the altitude from each of the three baselines).

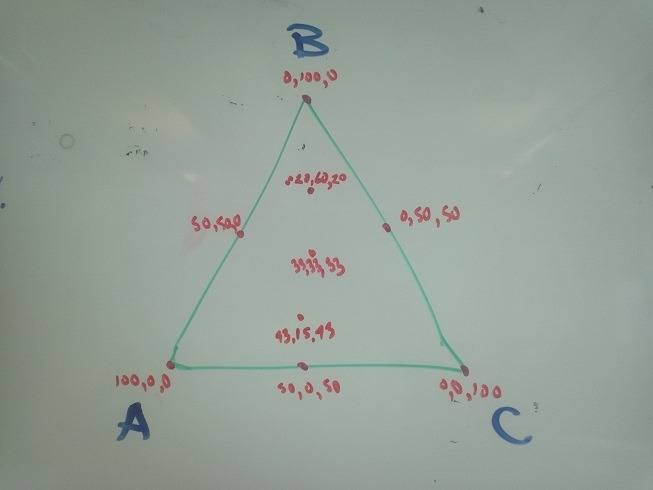
This works pretty well. The midpoint of a side will be some combination of 0,50,50. The dead centre will be 33,33,33. It's not a completely linear - or 1:1 - correlation between user movement and values - though it's close enough.

I just wonder if I'm missing some geometrical shape that's tailor-made for such a circumstance. I wonder if a circle would make more sense. But a circle doesn't have three apexes ... apex's ... apeces.

Ideas?

 

[mfb]

What is nonlinear? That triangle looks great if you want linearity in the transparency settings.

Human brains probably won't see that as linear - something at 100% doesn't look 100 times as prominent as something at 1%, especially if the image is much brighter than the other images. But that is a biology question.

 

[fresh_42]

If I understood it right and we may assume that opacity is always positive, then you have something like this:

 

[Ssnow]

Hi, it is interesting because your solution remember me a biological model called the Hardy-Weinberg law. In this model you have a constraint that is the sum of frequencies must be constant $p+q=1$ (in your case $100$) so taking the square $p^2+2pq+q^2=1$ where setting $l=p^2,m=2pq,n=q^2$ you have a parabola $m^2=4ln$ that is a parabola in $P^2$ (the projective space) that you can represent inside the triangle...
I don't know if I have understood clearly your problem but I think your geometry can be a parabola in the projective space (i.e. you describe a parabola inside your triangle with degenerate cases).

 

[DaveC426913]

View attachment 105878

Right, except if you have three axes of freedom, you would be allowed to set values for 100,100,100 or 0,0,0. You shouldn't be able to.

 

[DaveC426913]

What is nonlinear? That triangle looks great if you want linearity in the transparency settings.

Human brains probably won't see that as linear - something at 100% doesn't look 100 times as prominent as something at 1%, especially if the image is much brighter than the other images. But that is a biology question.

No, I'm not worried about that. The user never sees the numbers, just the effect. Not to mention that 100 increments is well below perception.

I guess the triangle is pretty near as perfect as I'm going to get.

Then it comes down to equations. Uhhh. hmmm...
altA = altitude(A | BC) (i.e. calculate the point's altitude when A is the triangle's peak and BC is its base)
altB = altitude(B | AC)
altC = altitude(C | AB)
sum = altA+altB+altC
value A = altA *100 / sum
value B = altB*100 / sum
value C = altC*100 / sum
Yeah. OK. So any point in the triangle gets normalized to a value set where A+B+C=100.

OK. So, for example, the centre bottom point:
altA = ~55
altB = ~20
altC = ~55
sum = 130
value A = 55*100/130 = 42
value B = 20*100/130 = 16
value C = 55*100/130 = 42

 

[DaveC426913]

Hi, it is interesting because your solution remember me a biological model called the Hardy-Weinberg law. In this model you have a constraint that is the sum of frequencies must be constant $p+q=1$ (in your case $100$) so taking the square $p^2+2pq+q^2=1$ where setting $l=p^2,m=2pq,n=q^2$ you have a parabola $m^2=4ln$ that is a parabola in $P^2$ (the projective space) that you can represent inside the triangle...
I don't know if I have understood clearly your problem but I think your geometry can be a parabola in the projective space (i.e. you describe a parabola inside your triangle with degenerate cases).

I'm ... not sure.

 

[fresh_42]

Right, except if you have three axes of freedom, you would be allowed to set values for 100,100,100 or 0,0,0. You shouldn't be able to.

No, I'm not having $(100,100,100)$ as a solution. The triangle in the figure is actually the part of a plane (given by $x_1OP_A+x_2OP_B+x_3OP_C = 100$) restricted to the first octant, i.e. opacity $\geq 0$.
What you propose is a cube, which I haven't drawn.
You have three axes of freedom plus the restriction by the linear (!) equation, which reduces the entire $3D-$space to the $2D-$plane. The additional positivity makes it a triangle.

 

[DaveC426913]

No, I'm not having $(100,100,100)$ as a solution. The triangle in the figure is actually the part of a plane (given by $x_1OP_A+x_2OP_B+x_3OP_C = 100$) restricted to the first octant, i.e. opacity $\geq 0$.
What you propose is a cube, which I haven't drawn.
You have three axes of freedom plus the restriction by the linear (!) equation, which reduces the entire $3D-$space to the $2D-$plane. The additional positivity makes it a triangle.

OK, that's what I thought maybe you were getting at.
The triangle is actually a 2D plane that intersects the axial planes, pitching and yawing through the space, constrained by the formula.

Unfortunately, I don't see how it would be intuitive to operate.
I mean, I can, I just don't think it makes for a very elegant control.

Well, unless it were symmetrical. Say if it were viewed from 45,45 degrees.

 

[mfb]

The user never sees the numbers, just the effect.

That still means the effect can look nonlinear with the linear joystick control.

If that occurs, there is a simple way to implement nonlinear effects while keeping the sum constant: apply the same nonlinear function to all three components, then divide by the sum (normalizing to 1 here)

As an example, consider f(x)=x^2. This slows the apperance of weak image components. If the user chooses the position (0.1, 0.4, 0.5), then applying the function gives (0.01, 0.16, 0.25), sum 0.42 => divide by 0.42 => new position (0.024, 0.381, 0.595).

 

[DaveC426913]

That still means the effect can look nonlinear with the joystick motion.

Yeah. I could apply a fudge factor.

 

[fresh_42]

Unfortunately, it's going to be pretty non-intuitive to operate, methinks.

Well, algorithmic you could start at $(OP_A,OP_B,OP_C) = (100,0,0)$ and change them by $(OP_A + x = 100)$ in $x-$direction and $(OP_A + y = 100)$ in $y-$direction of a joystick where $x$ represent $OP_B$ and $y$ represent $OP_C$.

 

[DaveC426913]

I can't help but wonder if there is a surface where any coords on it are always the sum of the distance from three points.

An elliptoid is a surface that is a fixed sum from two points.

But I guess I'd need a four-dimensioal hyper-elliptoid to have a such a surface using three points...

 

[fresh_42]

I can't help but wonder if there is a surface where any coords on it are always the sum of the distance from three points.

An elliptoid is a surface that is a fixed sum from two points.

But I guess I'd need a four-dimensioal hyper-elliptoid to have a such a surface using three points...

There is. E.g. https://en.wikipedia.org/wiki/N-ellipse
But you don't have three fixed points and a longer distance. Once you're in a corner, there's no room left over anymore.

 

[DaveC426913]

I can't help but wonder if there is a surface where any coords on it are always the sum of the distance from three points.

Derp. Of course there is. And it doesn't require more than 3 dimensions.

An equilateral triangle, that's "puffed" out the sides and top - like a 3-cornered pillow.
Any point on that surface will have vectors that add up to 100.

Thanks @fresh_42, looking at those n-polyellipses gave me the idea.

 

[DaveC426913]

I mean, it's purely academic. Unless I want some serious trigonometry happening in my joystick logic, I'm not going to have a 3D control on my page.

When it comes right down to it, I'll simply be viewing the triangle from above in two dimensions - exactly as in my original diagram - and the distances will be distorted a little.

 

[DaveC426913]

Nailed the dimensions to one decimal place. (Nothin' like doing trig longhand with a pencil & paper...)