chiralvandal
- 9
- 0
KE of a bar rotating at an angle- please help!
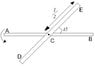
A slender prismatic bar DE Of length l(=1 m) and weight W(= 89 N) is rigidly attached at it's midpoint C to a shaft AB and makes an angle (alpha(=45degrees)) as shown in the figure. Find the kinetic energy T of the bar if it rotates with constant angular velocity (omega(=200 rpm)) about AB.
Work done= change in KE
and
Work done= integration of moments about the axis of rotation
I'm supposed to use the work- energy relation to solve this question but am clueless as to how to go about it... please help!
Homework Statement
A slender prismatic bar DE Of length l(=1 m) and weight W(= 89 N) is rigidly attached at it's midpoint C to a shaft AB and makes an angle (alpha(=45degrees)) as shown in the figure. Find the kinetic energy T of the bar if it rotates with constant angular velocity (omega(=200 rpm)) about AB.
Homework Equations
Work done= change in KE
and
Work done= integration of moments about the axis of rotation
The Attempt at a Solution
I'm supposed to use the work- energy relation to solve this question but am clueless as to how to go about it... please help!
Attachments
Last edited: