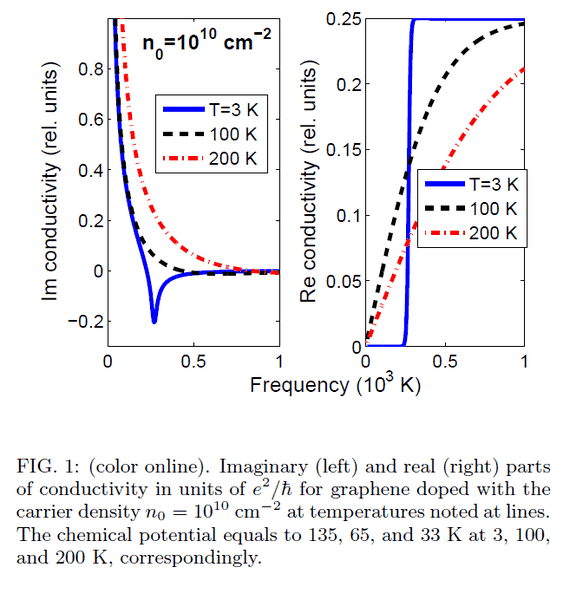
Discussion Overview
The discussion revolves around the transformation of frequency expressed in Kelvin units as presented in an article on the optical properties of graphene. Participants explore the implications of this unit transformation and seek clarification on the underlying principles and calculations involved.
Discussion Character
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
- Some participants suggest that the transformation from frequency to Kelvin is based on the relationship between energy, frequency, and temperature, specifically using the equations E = kbT and E = hv.
- Others question the validity of "dropping" constants like the Boltzmann constant (kb) and Planck's constant (h) in the transformation process, emphasizing the need to consider units carefully.
- A participant notes that what is reported as "frequency" may actually be expressed as ##\hbar \omega / k_\mathrm{B}##, indicating a specific relationship in the context of quantum mechanics.
- There is a discussion about the convenience of expressing quantities in terms of measurable units and the ability to convert between energy and temperature without losing meaning in the context of the same system.
Areas of Agreement / Disagreement
Participants express differing views on the appropriateness of dropping constants in unit transformations, indicating a lack of consensus on the method of conversion between frequency and temperature. Some agree on the conceptual framework, while others remain uncertain about the implications of the transformations.
Contextual Notes
There are unresolved questions regarding the assumptions made in the unit transformation and the dependence on specific definitions of energy and temperature in the context of the discussion.