- #1
- 3,385
- 2,636
The Sands of Duna
<Intermission (1/2)>
An intermission of math.
Skip this post (and the next) if you are not interested in the math. But since you are reading this on Physics Forums after all, there's a good chance you are interested. If so, read on.
Collinsmark is not affiliated with Squad nor Kerbal Space Program.
Here is the justification to some claims I've made in the last few posts, and the derivation to a couple equations.
It's a straightforward calculation to find the velocity of an object in a circular orbit around a much larger object. We simply set the acceleration of gravity equal to the centripetal acceleration.
[tex] \underbrace{\frac{v^2}{r}}_{\mathrm{centripetal}} = \underbrace{\frac{GM}{r^2}}_{\mathrm{gravitational}} [/tex]
Solving for [itex] v [/itex] gives us
[tex] v = \sqrt{\frac{GM}{r}} .[/tex]
By the way, when we assume that the smaller body, say our ship, is in orbit around a much larger body, like a moon or planet (or even the Sun), like we are doing here, it is called a restricted two-body problem. The assumption that the larger body is much, much more massive than the smaller is what makes it "restricted." So when you hear of a restricted two-body, restricted three-body, or restricted n-body problem, it means the mass of the ship is small compared to the mass of the other bodies being considered, and its effect on the motion of the larger body (or bodies) can be neglected.
We can also find the potential energy, U, of our ship when it is at some height above when orbiting a moon or planet. It is assumed that the potential energy, U, is zero when the ship is far, far away from the body. As the ship approaches the body, U, decreases, meaning it becomes more negative.
We can find this potential energy by integrating the force from its initial orbital height, up to infinity. In other words, we calculate the work required to slowly lift the ship from its present orbital height up to infinity.
[tex] W = \int \vec {F(r)} \cdot d \vec r [/tex]
Note that in our case, we are slowly moving the ship toward infinity, although the force is pointing in the opposite direction. That's where the negative sign comes from.
[tex] U = -\int_r^{\infty}G \frac{Mm}{{r'}^2} dr' [/tex]
Evaluating the integral gives us
[tex] U = - G \frac{Mm}{r} .[/tex]
The kinetic energy is the good 'ol [itex] T = \frac{1}{2}mv^2 [/itex], once we've chosen a suitable frame of reference. For the rest of this post, it's assumed that our frame of reference is that of the planet or moon the ship is orbiting, unless otherwise stated.
So the total energy of the ship is the ship's kinetic plus potential energy.
[tex] E = T + U = \frac{1}{2}mv^2 - G \frac{Mm}{r^2} [/tex]
It is often convenient to normalize this to energy per unit mass of the ship, by dividing by m. (This is particularly useful for those intervals of time when the ship is not burning any fuel and thus its mass remains constant.) That gives us
[tex] \epsilon = \frac{1}{2}v^2 - \frac{GM}{r},[/tex]
which brings us to our derivation of the standard escape equation in Figure 103.
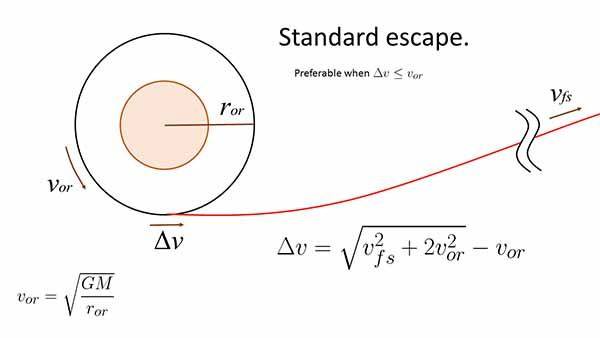
[Figure 103: Standard escape equation]
We know that eventually, when the ship is far away from the moon/planet, and traveling at its final, free-space velocity, [itex] v_{fs} [/itex] that its potential energy has dropped to zero. So in the end, the ship's total energy is all kinetic energy. Its initial (normalized) potential energy is simply [itex] -\frac{GM}{r_{or}} [/itex]. But what we don't know yet is its initial kinetic energy immediately after the burn. We know that before the burn, its orbital velocity is [itex] v_{or} [/itex]. Immediately after the burn, its velocity is [itex] v_{or} + \Delta v[/itex].
So we apply conservation of energy. We know that the ship's total energy is the same immediately after the burn as it is when the ship eventually reaches its final speed, [itex] v_{fs} [/itex].
[tex] \frac{1}{2} v_{fs}^2 = \frac{1}{2} \left( v_{or} + \Delta v \right)^2 - \frac{GM}{r_{or}} [/tex]
Substituting [itex] v_{or}^2 [/itex] in for [itex] \frac{GM}{r_{or}} [/itex] gives
[tex] \frac{1}{2} v_{fs}^2 = \frac{1}{2} \left( v_{or} + \Delta v \right)^2 - v_{or}^2. [/tex]
Multiplying by 2 and rearranging produces
[tex] \left( v_{or} + \Delta v \right)^2 = v_{fs}^2 + 2 v_{or}^2. [/tex]
And with a touch more algebra we find,
[tex] \Delta v = \sqrt{v_{fs}^2 + 2 v_{or}^2} - v_{or} [/tex]
which is the standard escape equation.
Note that when we take the derivative of [itex] \Delta v [/itex] with respect to [itex] v_{or} [/itex] and set that equal to zero, we find a minimum at [itex] v_{or} = \frac{v_{fs}}{\sqrt{2}} [/itex]. Plugging those back into our equation, we find that that minimum is [itex] \Delta v_{min} = v_{or} = \frac{v_{fs}}{\sqrt{2}} [/itex].
What that implies is that there is an optimal, orbital height for your ship to escape, if you are using the standard escape strategy (a single burn to escape). Assuming that you already know your final escape speed, the optimal orbital radius (for a circular orbit, and one you plan to use a standard escape with) is
[tex] r_{optimal} = 2 \frac{GM}{v_{fs}^2} [/tex]
Of course, KSP doesn't display orbital height in terms of radius to the center of the planet/moon. Rather it displays it as height above sea-level. So if you want to go by the height that KSP displays, you need to take the radius of planet/moon into account. Doing that gives
[tex] h_{optimal} = 2 \frac{GM}{v_{fs}^2} - r_{planet}[/tex]
where [itex] r_{planet} [/itex] is the radius of the moon/planet.
For every given planet or moon, you can find its radius and its standard gravitational parameter GM on the KSP wiki: http://wiki.kerbalspaceprogram.com/wiki/Main_Page.
You know that you have it right if you create a maneuver node in your present, circular orbit, for your desired destination, and the Δv displayed on the maneuver node equals (or nearly equals) your present orbital speed.
But what if you don't yet know your desired [itex] v_{fs} [/itex]? That's okay, you can calculate it. Create a maneuver node to your desired destination and jot down the Δv and your present orbital speed, [itex] v_{or} [/itex]. Then solve,
[tex] v_{fs} = \sqrt{ \left( v_{or} + \Delta v \right)^2 - 2 v_{or}^2} [/tex]
There's some serious implications to all of this. I've heard it said that "Minmus makes a great place to put a refueling station because it is near the edge of Kerbin's SOI, making it easier to escape." Ahh! No! That makes it a horrible place to put a refueling station, if you plan to escape the Kerbin system using the standard escape strategy.* With a standard escape, you'll use less fuel escaping if you start from a lower orbit.
*(There is one exception to this: asteroids. Asteroids travel in nearly the same orbit as Kerbin, so the ship's [itex] v_{fs} [/itex] is almost zero, with respect to Kerbin. So yes, a Minimus output would work quite well for asteroid redirect missions. But that's about it, if you limit yourself to standard escapes. On the other hand, if you want to use the fancy-shmancy escape, Minmus has advantages because it is so high above Kerbin. More on that in the next post.)
And, when using the standard escape, the ideal orbital height is closer to Kerbin, the farther the destination is, orbital wise. Putting it another way, the greater [itex] v_{fs} [/itex], the optimal orbital height is lower, all else the same (assuming standard escape).
If you work out the math, you'll find that the Mun would make a great place for a refueling station for the purpose of going to Duna, using a Hohmann transfer to Duna (Minmus is way to high for a standard escape to Duna). For planets that are farther way than Duna, even the Mun is too high for an optimal, Direct escape. So for planets beyond Duna, either put your refueling stations in a lower Kerbin orbit, or be prepared to do the fancy-shmancy via Kerbin, on the way out of the system.
The things to take home with you regarding the standard escape are:
[Edit: By the way, for the record, I am not a big fan of having refueling stations around Kerbin. They will invariably require more fuel used, overall, if you take into account the cost of getting the stations into orbit in the first place, and all the fuel needed to put the remaining fuel in orbit. That said, refueling stations can have tremendous advantages around systems with multiple moons like Jul. And if you ever attempt to take off from Eve (a large, gravitationally strong planet), you'll definitely want some fuel waiting in orbit. I know that many KSP players are fans of single-ship (or single-stage) to orbit (SSTO) crafts, and while I've never been a big fan of SSTOs, refueling stations can also be good for those.]
<Intermission (1/2)>
An intermission of math.
Skip this post (and the next) if you are not interested in the math. But since you are reading this on Physics Forums after all, there's a good chance you are interested. If so, read on.
Collinsmark is not affiliated with Squad nor Kerbal Space Program.
Here is the justification to some claims I've made in the last few posts, and the derivation to a couple equations.
It's a straightforward calculation to find the velocity of an object in a circular orbit around a much larger object. We simply set the acceleration of gravity equal to the centripetal acceleration.
[tex] \underbrace{\frac{v^2}{r}}_{\mathrm{centripetal}} = \underbrace{\frac{GM}{r^2}}_{\mathrm{gravitational}} [/tex]
Solving for [itex] v [/itex] gives us
[tex] v = \sqrt{\frac{GM}{r}} .[/tex]
By the way, when we assume that the smaller body, say our ship, is in orbit around a much larger body, like a moon or planet (or even the Sun), like we are doing here, it is called a restricted two-body problem. The assumption that the larger body is much, much more massive than the smaller is what makes it "restricted." So when you hear of a restricted two-body, restricted three-body, or restricted n-body problem, it means the mass of the ship is small compared to the mass of the other bodies being considered, and its effect on the motion of the larger body (or bodies) can be neglected.
We can also find the potential energy, U, of our ship when it is at some height above when orbiting a moon or planet. It is assumed that the potential energy, U, is zero when the ship is far, far away from the body. As the ship approaches the body, U, decreases, meaning it becomes more negative.
We can find this potential energy by integrating the force from its initial orbital height, up to infinity. In other words, we calculate the work required to slowly lift the ship from its present orbital height up to infinity.
[tex] W = \int \vec {F(r)} \cdot d \vec r [/tex]
Note that in our case, we are slowly moving the ship toward infinity, although the force is pointing in the opposite direction. That's where the negative sign comes from.
[tex] U = -\int_r^{\infty}G \frac{Mm}{{r'}^2} dr' [/tex]
Evaluating the integral gives us
[tex] U = - G \frac{Mm}{r} .[/tex]
The kinetic energy is the good 'ol [itex] T = \frac{1}{2}mv^2 [/itex], once we've chosen a suitable frame of reference. For the rest of this post, it's assumed that our frame of reference is that of the planet or moon the ship is orbiting, unless otherwise stated.
So the total energy of the ship is the ship's kinetic plus potential energy.
[tex] E = T + U = \frac{1}{2}mv^2 - G \frac{Mm}{r^2} [/tex]
It is often convenient to normalize this to energy per unit mass of the ship, by dividing by m. (This is particularly useful for those intervals of time when the ship is not burning any fuel and thus its mass remains constant.) That gives us
[tex] \epsilon = \frac{1}{2}v^2 - \frac{GM}{r},[/tex]
which brings us to our derivation of the standard escape equation in Figure 103.
[Figure 103: Standard escape equation]
We know that eventually, when the ship is far away from the moon/planet, and traveling at its final, free-space velocity, [itex] v_{fs} [/itex] that its potential energy has dropped to zero. So in the end, the ship's total energy is all kinetic energy. Its initial (normalized) potential energy is simply [itex] -\frac{GM}{r_{or}} [/itex]. But what we don't know yet is its initial kinetic energy immediately after the burn. We know that before the burn, its orbital velocity is [itex] v_{or} [/itex]. Immediately after the burn, its velocity is [itex] v_{or} + \Delta v[/itex].
So we apply conservation of energy. We know that the ship's total energy is the same immediately after the burn as it is when the ship eventually reaches its final speed, [itex] v_{fs} [/itex].
[tex] \frac{1}{2} v_{fs}^2 = \frac{1}{2} \left( v_{or} + \Delta v \right)^2 - \frac{GM}{r_{or}} [/tex]
Substituting [itex] v_{or}^2 [/itex] in for [itex] \frac{GM}{r_{or}} [/itex] gives
[tex] \frac{1}{2} v_{fs}^2 = \frac{1}{2} \left( v_{or} + \Delta v \right)^2 - v_{or}^2. [/tex]
Multiplying by 2 and rearranging produces
[tex] \left( v_{or} + \Delta v \right)^2 = v_{fs}^2 + 2 v_{or}^2. [/tex]
And with a touch more algebra we find,
[tex] \Delta v = \sqrt{v_{fs}^2 + 2 v_{or}^2} - v_{or} [/tex]
which is the standard escape equation.
Note that when we take the derivative of [itex] \Delta v [/itex] with respect to [itex] v_{or} [/itex] and set that equal to zero, we find a minimum at [itex] v_{or} = \frac{v_{fs}}{\sqrt{2}} [/itex]. Plugging those back into our equation, we find that that minimum is [itex] \Delta v_{min} = v_{or} = \frac{v_{fs}}{\sqrt{2}} [/itex].
What that implies is that there is an optimal, orbital height for your ship to escape, if you are using the standard escape strategy (a single burn to escape). Assuming that you already know your final escape speed, the optimal orbital radius (for a circular orbit, and one you plan to use a standard escape with) is
[tex] r_{optimal} = 2 \frac{GM}{v_{fs}^2} [/tex]
Of course, KSP doesn't display orbital height in terms of radius to the center of the planet/moon. Rather it displays it as height above sea-level. So if you want to go by the height that KSP displays, you need to take the radius of planet/moon into account. Doing that gives
[tex] h_{optimal} = 2 \frac{GM}{v_{fs}^2} - r_{planet}[/tex]
where [itex] r_{planet} [/itex] is the radius of the moon/planet.
For every given planet or moon, you can find its radius and its standard gravitational parameter GM on the KSP wiki: http://wiki.kerbalspaceprogram.com/wiki/Main_Page.
You know that you have it right if you create a maneuver node in your present, circular orbit, for your desired destination, and the Δv displayed on the maneuver node equals (or nearly equals) your present orbital speed.
But what if you don't yet know your desired [itex] v_{fs} [/itex]? That's okay, you can calculate it. Create a maneuver node to your desired destination and jot down the Δv and your present orbital speed, [itex] v_{or} [/itex]. Then solve,
[tex] v_{fs} = \sqrt{ \left( v_{or} + \Delta v \right)^2 - 2 v_{or}^2} [/tex]
There's some serious implications to all of this. I've heard it said that "Minmus makes a great place to put a refueling station because it is near the edge of Kerbin's SOI, making it easier to escape." Ahh! No! That makes it a horrible place to put a refueling station, if you plan to escape the Kerbin system using the standard escape strategy.* With a standard escape, you'll use less fuel escaping if you start from a lower orbit.
*(There is one exception to this: asteroids. Asteroids travel in nearly the same orbit as Kerbin, so the ship's [itex] v_{fs} [/itex] is almost zero, with respect to Kerbin. So yes, a Minimus output would work quite well for asteroid redirect missions. But that's about it, if you limit yourself to standard escapes. On the other hand, if you want to use the fancy-shmancy escape, Minmus has advantages because it is so high above Kerbin. More on that in the next post.)
And, when using the standard escape, the ideal orbital height is closer to Kerbin, the farther the destination is, orbital wise. Putting it another way, the greater [itex] v_{fs} [/itex], the optimal orbital height is lower, all else the same (assuming standard escape).
If you work out the math, you'll find that the Mun would make a great place for a refueling station for the purpose of going to Duna, using a Hohmann transfer to Duna (Minmus is way to high for a standard escape to Duna). For planets that are farther way than Duna, even the Mun is too high for an optimal, Direct escape. So for planets beyond Duna, either put your refueling stations in a lower Kerbin orbit, or be prepared to do the fancy-shmancy via Kerbin, on the way out of the system.
The things to take home with you regarding the standard escape are:
- There is an optimal, orbital height for entering and leaving a system for a given [itex] v_{fs} [/itex], when using the standard arrival or standard escape (single burn). This is great place to park massive service modules and massive refueling stations. Parking massive service modules/refueling stations in other orbital heights, either higher or lower, will require the ships to burn more fuel on arriving and escaping, assuming the standard arrival or standard escape (single burn).
- This optimal height is dependent on the destination. More correctly, it is dependent on the [itex] v_{fs} [/itex] needed when escaping the system. (Assuming that the same type of orbit is used on arriving, the arrival [itex] v_{fs} [/itex] should be the same as the escape [itex] v_{fs} [/itex], btw.) And of course it is also dependent on the standard gravitational parameter, GM, of the moon/planet you are orbiting.
- All that said, there is the potential to save even more fuel by parking in yet higher orbits, if you use the fancy-shmancy arrival/escape, which we'll talk about in the second half of the intermission.
[Edit: By the way, for the record, I am not a big fan of having refueling stations around Kerbin. They will invariably require more fuel used, overall, if you take into account the cost of getting the stations into orbit in the first place, and all the fuel needed to put the remaining fuel in orbit. That said, refueling stations can have tremendous advantages around systems with multiple moons like Jul. And if you ever attempt to take off from Eve (a large, gravitationally strong planet), you'll definitely want some fuel waiting in orbit. I know that many KSP players are fans of single-ship (or single-stage) to orbit (SSTO) crafts, and while I've never been a big fan of SSTOs, refueling stations can also be good for those.]
Last edited: