How Do I Solve This Complex Kinematics Displacement Problem?

[soccerjayl]

Encountered the following question. For (a), I repetitively found the answer 12 for magnitude of displacement and 131° for the direction; after being told i was incorrect...i need help:

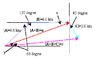
Path A is 8.0 km long heading 60.0° north of east. Path B is 6.0 km long in a direction due east. Path C is 3.0 km long heading 315° counterclockwise from east.

(a) Graphically add the hiker's displacements in the order A, B, C.

What is the magnitude of displacement (km)? What is the direction of displacement (°counterclockwise from East)?

(b) Graphically add the hiker's displacements in the order C, B, A.

What is the magnitude of displacement (km)? What is the direction of displacement (°counterclockwise from East)?

(c) What can you conclude about the resulting displacements?


thanks.

 

[Leong]

Sine & Cosine Laws

a=\sqrt{6^2+8^2-2*6*8*cos\ 120}
a=\sqrt{148}

\frac{sin\ x}{8}=\frac{sin\ 120}{\sqrt{148}}
x = 35^0

c=\sqrt{3^2+148-2*3*\sqrt{148}*cos\ 100}
c=13\ km

\frac{sin\ y}{3}=\frac{sin\ 100}{13}
y = 13^0
The direction is (35-13)=22 degree

 

[soccerjayl]

a=\sqrt{6^2+8^2-2*6*8*cos\ 120}
a=\sqrt{148}

\frac{sin\ x}{8}=\frac{sin\ 120}{\sqrt{148}}
x = 35^0

c=\sqrt{3^2+148-2*3*\sqrt{148}*cos\ 100}
c=13\ km

\frac{sin\ y}{3}=\frac{sin\ 100}{13}
y = 13^0
The direction is (35-13)=22 degree

i don't know what level physics that is...

but I am in 11th grade honors...

its the right answer, but i have no explanation

i'm used to the more adding/subtracting vectors, forming pictures and finding the resultants using trig functions...

but thanks, you did help

 

[decibel]

you don't know the sine and cosine law?

 

[soccerjayl]

i know this...but no i haven't reached class with emphasis on trig

sin(angle)=opposite/hypo

cos(angle)=adjacent/hypo

im guessin that's not enough?

 

[Pyrrhus]

Using Cosine Law and Sine Law is a way.

You can get the magnitude and direction of the resultant vector (\vec{R}) by using the components.

\vec{R} = (R_{x}i + R_{y}j)
\vec{A} = (8 , 60^o)
\vec{B} = (6, 0^o)
\vec{C} = (3, 315^o)

R_{x} = (A_{x} + B_{x} + C_{x})i
R_{y} = (A_{y} + B_{y} + C_{y})j

A_{x} = 8\cos(60^o) = 4
B_{x} = 6\cos(0^o) = 6
C_{x} = 3\cos(315^o)= 2.12

A_{y} = 8\sin(60^o) = 6.93
B_{y} = 6\sin(0^o) = 0
C_{y} = 3\sin(315^o) = -2.12

\vec{R} = (12.12i + 4.81j)

|\vec{R}| = \sqrt{R_{x}^2+R_{y}^2}
|\vec{R}| = 13.04
\theta_R = arctan(\frac{R_{y}}{R_{x}})
\theta_R = 21.65^o

-Cyclovenom

 

[soccerjayl]

thanks..

makes much more sense