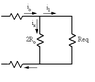The discussion revolves around solving a parallel circuit problem using Kirchhoff's Laws. The original poster is struggling with calculations in parts A and B, specifically regarding the equivalent resistance and the correct application of Kirchhoff's rules. Clarifications are provided about the relationships between resistances and currents, emphasizing the importance of using correct units and understanding the current divider principle. The conversation highlights the need to accurately represent the circuit and apply Kirchhoff's Current Law (KCL) to find the current distribution. Ultimately, the participants aim to resolve the confusion and arrive at the correct solution for the circuit problem.