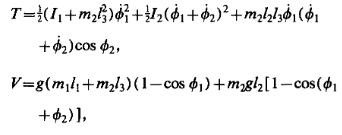SUMMARY
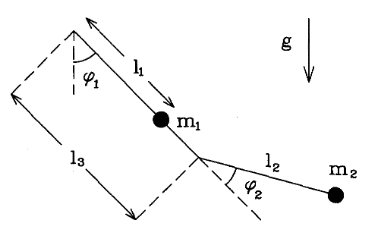
The discussion focuses on deriving the Lagrangian for a double undamped pendulum, specifically addressing the complexities introduced by the second angle φ2, which is measured from the line connecting the two pivot points. Participants suggest using the kinetic energy equations, T = (1/2) m1(ẋ1² + ẏ1²) + (1/2) m2(ẋ2² + ẏ2²), and emphasize the importance of calculating the velocities of the pendulum masses in terms of their angles. The conversation concludes with a confirmation that the calculations align with the expected results, particularly in simplifying the dot product of the position vectors.
PREREQUISITES
- Understanding of Lagrangian mechanics
- Familiarity with kinetic energy equations
- Knowledge of vector calculus
- Ability to perform algebraic manipulations involving trigonometric functions
NEXT STEPS
- Study the derivation of the Lagrangian for multi-body systems
- Learn about the application of the Euler-Lagrange equation in dynamics
- Explore the concept of generalized coordinates in Lagrangian mechanics
- Investigate the effects of damping in pendulum systems
USEFUL FOR
Students and professionals in physics, particularly those specializing in classical mechanics, as well as engineers working on dynamic systems and simulations involving pendulum motions.