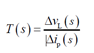Laplace Transform of the input portion of this circuit

[Jason-Li]

Homework Statement

a) Draw the Laplace form of the input portion of the circuit, as
represented in FIGURE 4(c).

b) Derive an expression for the Laplace transfer function as per figure 4(c).

I have attached the transfer function & figure 4 (c) in my attempt.

Relevant Equations

Standard look up tables for Laplace

So I have completed (a) as this (original on the left):

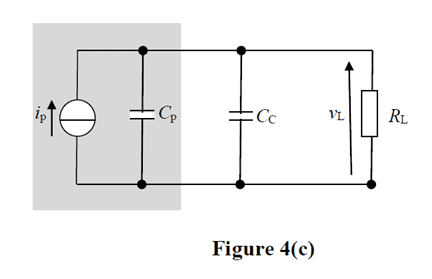
I have then went onto (b) and I have equated T(s)=Z(s) as follows:

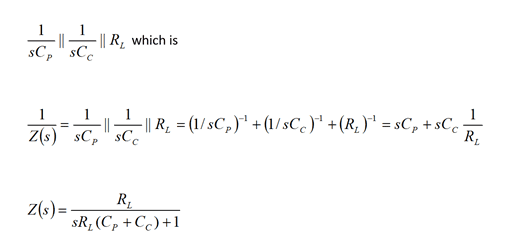
and due to

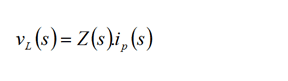
hence

Does this look correct to you smarter people?

Thanks in advance! All replies are welcome :)

 

[Jody]

Are you trying to solve for the circuit in phasor form?

The results look right to me if it's just phasor form. There's a step where things look a little confusing by my eye. This part below looks concerning to me although it appears less concerning later on the right side.

$${1 \over Z(s)} = {1 \over {sC_p}} \parallel {1 \over {sC_s}} \parallel R_L$$

When I read about Laplace transforms (including standard lookup tables among your relevant equations)... I'm actually expecting a transform from $s$ to $t$ or its converse. The one on the table I'd be looking at is in this form although you'll have to massage the equation (a little bit) on your own if you do require the additional steps.

$$e^{-at} \leftrightarrow {1 \over {s + a}}$$

 

[rude man]

Your transform is $V_L (s)/(I_p(s).$ You should be using conductance G(s), susceptance B(s) and admittance Y(s) = G + jB(s) rather than impedance Z = R + jX(s). That is suggested by the all-parallel nature of the circuit. You need to think in these terms if the math is thereby greatly simplified. Similarly, use Norton's therem for the input section.

Anyway, your answer is correct. But think G, B and Y whenever a circuit has lots of loops and few independent nodes.