Jeff12341234
- 179
- 0
1. The limit as b approaches infinity always shows up as undefined on my calc so I don't know what to put for that section of the work.
2. What pat of the work is supposed to need L'hopital's rule? The integration?
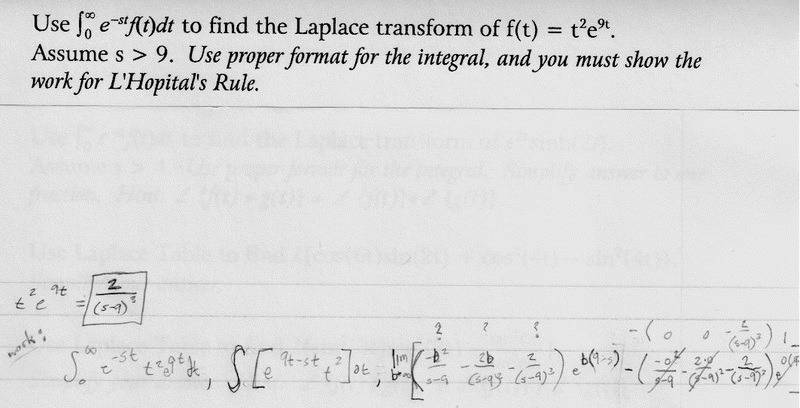
2. What pat of the work is supposed to need L'hopital's rule? The integration?