Akuu
- 3
- 0
Speed of a bullet shot into a pendulum ,picture included (dl attch. if pic won't show)
You're supposed to be able to define the speed of a bullet with the help of a pendulum.
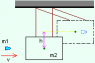
The bullet is shot into a big tree piece ( The pendulum ) with a known mass (weight). The tree piece's center of gravity is lifted upwards when hit by the bullet. What is the speed of the bullet if the bullet's mass (weight) is 7.5g ( 0.0075 kg ), the tree piece's mass (weight) is 4.3 kg and the tree piece is lifted upwards in height of 8.8 cm ( 0.088 m )?
bullet: m1 = 7.5 g = 0.0075 kg :: v (speed) = ? ( This is the question )
tree piece: m2 = 4.3 kg ( it is the pendulum, see picture below )
height: h = 8.8 cm = 0.088 m ( the length that the tree piece is lifted upwards ).

E(sum) p (before) = E(sum) p (after)
m1v1 + m2v2 = m1u1 + m2u2,
- where m1v1 and m2v2 are 'motion quantity' before the collision whereas m1u1 and m2u2 are the 'motion quantity' after the collision.
I think this is what they want me to use.
Ok I've been trying at this for a while now but I can't figure out what to DO with the HEIGHT that is given ( tree piece lifted 8.8 cm ). I can't find a way to define the length the tree piece moves right on the x-plane.
Basically all solutions I've come up with have all been wrong. I tried to use the "Law to preserve energy", the one with E(potential) = E(kinetic) But it didn't work out either.
THE CORRECT ANSWER SHOULD BE: 'v = 4.6 m/s'
Any TIPS on how to solve this? Thanks in advance.
Homework Statement
You're supposed to be able to define the speed of a bullet with the help of a pendulum.
The bullet is shot into a big tree piece ( The pendulum ) with a known mass (weight). The tree piece's center of gravity is lifted upwards when hit by the bullet. What is the speed of the bullet if the bullet's mass (weight) is 7.5g ( 0.0075 kg ), the tree piece's mass (weight) is 4.3 kg and the tree piece is lifted upwards in height of 8.8 cm ( 0.088 m )?
bullet: m1 = 7.5 g = 0.0075 kg :: v (speed) = ? ( This is the question )
tree piece: m2 = 4.3 kg ( it is the pendulum, see picture below )
height: h = 8.8 cm = 0.088 m ( the length that the tree piece is lifted upwards ).
Homework Equations
E(sum) p (before) = E(sum) p (after)
m1v1 + m2v2 = m1u1 + m2u2,
- where m1v1 and m2v2 are 'motion quantity' before the collision whereas m1u1 and m2u2 are the 'motion quantity' after the collision.
I think this is what they want me to use.
The Attempt at a Solution
Ok I've been trying at this for a while now but I can't figure out what to DO with the HEIGHT that is given ( tree piece lifted 8.8 cm ). I can't find a way to define the length the tree piece moves right on the x-plane.
Basically all solutions I've come up with have all been wrong. I tried to use the "Law to preserve energy", the one with E(potential) = E(kinetic) But it didn't work out either.
THE CORRECT ANSWER SHOULD BE: 'v = 4.6 m/s'
Any TIPS on how to solve this? Thanks in advance.
Attachments
Last edited: