djkinney
- 8
- 0
Homework Statement
Suppose that, while lying on a beach near the equator of a far-off planet watching the sun set over a calm ocean, you start a stopwatch just as the top of the sun disappears. You then stand, elevating your eyes by a height H = 1.58 m, and stop the watch when the top of the sun again disappears. If the elapsed time is t = 10.9 s, what is the radius r of the planet to two significant figures? Notice that duration of a solar day at the far-off planet is the same that is on Earth.
Homework Equations
86400 s=1 day
The Attempt at a Solution
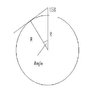
I attempted to solve this by setting the angle, but I think I got the wrong angle. (.0454°)
cos(0.0454°)=((r)/(r+h)) h=1.58
When I solved for the radius I got 1.5e^3, but it is not the right answer. Please help me figure where I went wrong! Thank you!