Lasha
- 25
- 0
So this is the circuit(with equations which were written by me, so I don’t know if they’re correct)
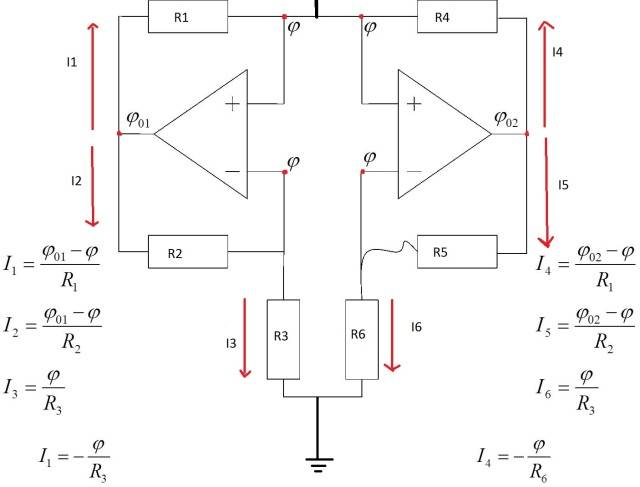
and this is the graph I should get, but I don’t know how.( g(x) is the current vs resistance)
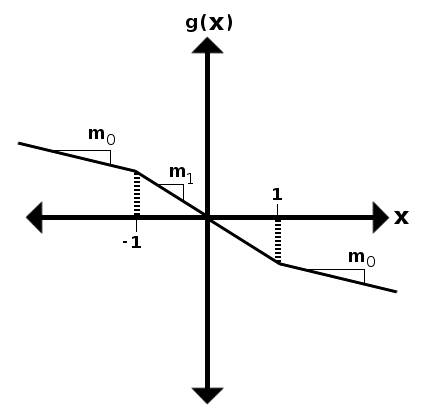
I assume that those two equations collide somehow and I get that g(x), but I’m not sure.
So my question is: how do I get that g(x) with that circuit?
thanks
and this is the graph I should get, but I don’t know how.( g(x) is the current vs resistance)
I assume that those two equations collide somehow and I get that g(x), but I’m not sure.
So my question is: how do I get that g(x) with that circuit?
thanks