L'Hopital on limit of tanx(lnx) as x ->0 (from the right).

[LearninDaMath]

L'Hopital on limit of tanx(lnx) as x -->0 (from the right).

Regarding this solution to the lim of (tanx)(lnx) as x approaches zero (from the right).

I'm confused about the part I outlined in blue:

What steps are going on here?

 

[emailanmol]

You can solve it in two steps if you write it as ln(x)/cot(x) amd now differentiate.


You get -1/x*cosec^2(x)
I.e -sin^2(x)/x


What do you see?

 

[emailanmol]

Although the test book has got the right answer, the step where it takes the limit of sec^2(x) seperately is not allowed (it doesn't make a difference here.But it can on other questions).

You can also continue the textbook way amd differentiate the numerator sec^2(x)*(ln(x))^2 with chain rule but it gets really complicated and requires high observation to get the right limit.

 

[LearninDaMath]

I get what you are saying. You are saying that to start with a different fraction altogether before applying Lhopitals would take much less steps.

However, I'd really like to know about this particular method. Even though it takes more steps, I'd like to understand how its accomplished. I don't understand the algebraic steps that are skipped within the part I oulined in blue.EDIT: This post is in response to your first reply. I didn't see your second post at the time I made this post. I'm going to make another post in reply to your second reply.

 

[emailanmol]

Ok sure. :-)
Just to provide you with more insights.

You can also write tan(x)*ln(x) as x*ln(x)
as limit x-> 0,
tanx=x

This also solves in two steps with some good obervation :-)

 

[LearninDaMath]

I could rewrite (sec^2(x)*(ln(x))^2)/(1/x) as:

\lim_{x \to +\infty} \frac{x(lnx)^{2}}{-cos^{2}x} = ∞/∞

Applying L'Hopitals gives:

\frac{2lnx(\frac{1}{x})}{\frac{cosx(cosx+2xsinx}{x^2}}

And then applying the limit as x -->0 gives ∞/∞ again.

But applying L'Hopital again just seems like it will get really complicated as you say.

-----------------------------------------------------------------------------------------

So I have a few questions. The first question(s): Why is the the step where it takes the limit of sec^2(x) seperately not allowed? In what instance does it make a difference?

Second question: What do you mean by high observation?

Third and probably most pertenant question:

How do you know which fraction to set the function into in order to end up with the least complicated Lhopital steps? I mean, I understand which two fractions I can make. But how do I know which fraction to actually proceed with LHopitals rule? For instance, is there any unwritten rules of thumb that makes life easier such as if you have a trig function, make sure to put it into the denominator instead of the numerator (or visa versa) when applying Lhopitals? Or when you have lnx, its best to make sure when you put it into fraction form, to put it in the numerator?

I understand that you need to have the form 0/0 or ∞/∞, but how do I know which fraction form of a particular function is going to be the easiest form to proceed with?

It feels like someone who's good at chess can see 20 steps ahead so they just "know" which way will be less complicated. But as a beginner, how do I know to choose ln(x)/cot(x) as the easier route instead of what I (and the solution I posted) chose?

I know that 3rd set of questions turned into a bunch of questions asking pretty much the same thing in different ways, but i just want to be specific so I'm sure I'm correctly explaining my confusion/question.

 

[emailanmol]

Hey,

Great questions.


I will answer your second and third question now and try to lcome up with a suitable example for the first later in the post.

Beginning with question 3:

Yes it is like chess and it comes up with experience (not a lot of experience ks required cause I am in high school too :-) )and some luck too!

Read my comments (and other members' too) here
https://www.physicsforums.com/showthread.php?t=588408


The general way is to switch methods when one way is getting way too long.

There is no fixed rule or order.
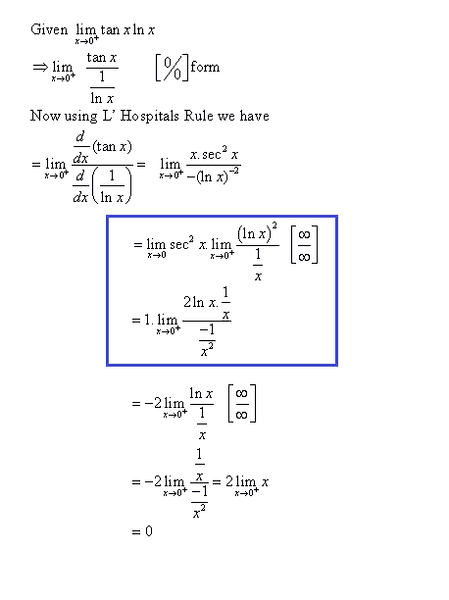
The only thing you should remember is to avoid to differentiate a function like g(x)/f(x)

(1/ln(x) was such a function in our question)

It leads to way too many terms.

I usually do a rough math in my head first to see what all possible functions pop up in the first few steps and then I write on paper the exact steps to obtain the answer.
I think a lot , and even after I have obtained an answer I keep looking for other methods .

Like in this question i saw that (i have to make a 0/0 or infinity by infinity) tanx has a much more elegant reciprocal cotx which when goes down produces a simple function -cosec^2x on differentiation so i went that way.


There is no thumb rule.
Key is to think for a few seconds before attempting and to plan your assault.




Answering question 2

Observation is really very important.At every stage you have think of a quick exit to solution or some manipulation which can help decrease calculation.

Suppose the value of limit is y

so y=sec^2(x)*ln(x)^2/(1/x)
Y=sec^2(x)*ln(x)^2*x

Now as x tends to zero x=tan x
So y =sec^2(x)*ln(x)^2*tan(x)
y=sec^2(x)*lnx*y

(Remember y=lnx*tanx)

y(1-sec^2(x)ln(x))=1
y=1/(1-sec^2(x)ln(x))=0.




All steps may seem very arbitrary right now and like a very lucky guess
(and to certain extent it is),

but with practice (and some slight changes in thinking ) they are easy to interpret.


For the first question look at
x^2/tan^x (x tends to 0).
Its value is 1.

However if you take an
x out it becomes

Lt (x) Lt (x/tan^2x)

which yields half on differentiation which is wrong.

 

[LearninDaMath]

Appreciate your feedback. Can you elaborate a bit on your reply to question 2

Answering question 2

Observation is really very important.At every stage you have think of a quick exit to solution or some manipulation which can help decrease calculation.

Suppose the value of limit is y

so y=sec^2*ln(x)^2/(1/x)
Y=sec^2*ln(x)^2*x

Now as x tends to zero x=tan x
So y =sec^2*ln(x)^2*tan(x)
y=sec^2(x)*lnx*y

(Remember y=lnx*tanx)

y(1-sec^2(x)ln(x))=1
y=1/(1-sec^2(x)ln(x))=0.

Specifically, I don't understand some of the steps. For instance, I don't understand the statement "as x tends to zero x = tanx." How is this observation made?

 

[emailanmol]

What is limit of x/tanx when x tends to 0?

Also I have edited my post .
Many places i had written sec^2 instead of sec^2(x) by mistake.

 

[LearninDaMath]

What is limit of x/tanx when x tends to 0?

Also I have edited my post .
Many places i had written sec^2 instead of sec^2(x) by mistake.

Edit noted, thanks.


the limit of x/tanx when x tends to 0 is 1, right? and that is because 0/0 is indeterminent and h'lopitals rule makes 1(cos^2(x))

 

[emailanmol]

Yes, Correct.


So when x tends to 0,
we have x/tanx=1
i.e. x=tanx
which is exactly what I have used.

 

[LearninDaMath]

Yes, Correct.


So when x tends to 0,
we have x/tanx=1
i.e. x=tanx
which is exactly what I have used.

Okay, so you're saying that whenever there is a limit of a function as x tends to zero, I can substitute tanx for a given x if it helps to simplify the function? If I am understanding your explanation correctly, then wow, that is pretty neat.

Oh and by the way, I'm not in high school. I'm in college calculus. And unfortunately, I did not realize how interesting math was in high school and avoided it at all costs. So I didn't take calculus (or much of any other maths) in high school. However, since you are currently taking high school calculus, may I ask, has this specific technique of solving a separate limit in order to make a substitution into another limit ever been covered in high school calculus? I ask because a technique of this type has never been mentioned in my calculus class.

Of course this thread is on the topic of evaluating a L'hopital by the less ideal route, and perhaps the need for the technique you have shown most likely would not be necessary if I had just written ln(x)/cot(x) as you originally stated. However, I still wonder, is this technique covered/discussed/learned in high school calc?

Thanks.

 

[emailanmol]

Yes.Thats exactly what i meant that you can substitute tan x and x with each other.


Actually none of these methods were discussed in my class.I have formulated most of them myself. :-)

 

[emailanmol]

And don't worry differential calculus is pretty easy.You will catch up what you missed in no time at all.

 

[LearninDaMath]

Yes.Thats exactly what i meant that you can substitute tan x and x with each other.

Cool thanks.

Actually none of these methods were discussed in my class.I have formulated most of them myself. :-)

Nice!

And don't worry differential calculus is pretty easy.You will catch up what you missed in no time at all.

I hope so. I feel like I'm making a lot of progress at a pretty good pace. Upon graduating high school, if i'd have been asked what's a general equation that describes a simple straight line, I would have responded with, "I don't know, is stuff really all that important anyways?" I can't go back in time, but I'm trying to make the best use of my time in the present. Anyway thanks for your help.

 

[emailanmol]

Your welcome :-)

My conditions pretty much the same in Chemistry.