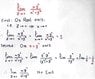Limited Value in Compound Functions: Remembering Number Paths

[m_s_a]

When we think a value an end in the compound functions :
We remember that we in front of number from not a limited from the paths

 

[Dick]

We remember that we in back of path from not a limited from the numbers. Is that wrong? I really can't understand you. Sorry.

 

[m_s_a]

We remember that we in back of path from not a limited from the numbers. Is that wrong? I really can't understand you. Sorry.

He is not at the end a presence
Why ؟
The previous way the others is suitable ? why ?...
Look please:

 

[Dick]

He is not at the end a presence
Why ؟
The previous way the others is suitable ? why ?...
Look please:

I will. When it's approved. I think that gives me time to get a good night's sleep.

 

[Dick]

He is not at the end a presence
Why ؟
The previous way the others is suitable ? why ?...
Look please:

Now I don't understand what your picture is trying to tell me either. The proof of the limit in your first post is just fine.

 

[m_s_a]

Now I don't understand what your picture is trying to tell me either. The proof of the limit in your first post is just fine.

I did not understand your intention ?
I do not have a confirmation of the response
But look at the next example:
I apologize
Second : on the axis z = y^2

 

[HallsofIvy]

You have now posted 3 different pictures that appear to involve three different problems. As Dick told you before, the first is correct. This third one is also correct- except for spelling: since you get two different limits by approaching (0,0) along two different paths, the limit does not exist.

I'm not sure what the second picture was supposed to represent. But one thing you should be careful about: The line y= 2x, for example, in R², is not in the complex plane.

 

[m_s_a]

You have now posted 3 different pictures that appear to involve three different problems. As Dick told you before, the first is correct. This third one is also correct- except for spelling: since you get two different limits by approaching (0,0) along two different paths, the limit does not exist.
My answer of the first question :
is correct or a mistake?


I'm not sure what the second picture was supposed to represent. But one thing you should be careful about: The line y= 2x, for example, in R², is not in the complex plane.

My answer of the first question :
is correct or a mistake?


remember:
x=(z+z')/2
y=(z-z')/2i
z'=z par

 

[Dick]

lim(z->0) is not the same as lim(x->0) or lim(y->0). It's lim(x->0 AND y->0).

 

[m_s_a]

lim(z->0) is not the same as lim(x->0) or lim(y->0). It's lim(x->0 AND y->0).

Look into the proof of Coshi theory - Riman

f'(z)=f'(x)=f'(y)


no f'(z)=f'(x)+f'(y)

 

[Dick]

Look into the proof of Coshi theory - Riman

f'(z)=f'(x)=f'(y)


no f'(z)=f'(x)+f'(y)

What have derivatives got to do with it? You were posting limit problems. Or something. I give up. I don't know what your question or problem is.

 

[m_s_a]

I support the second solution
And I am not sure

 

[Dick]

If you are asking does |z|^2/z approach 0 as z approaches 0. Then, it does. You're first argument is fine. If you think there is a problem because the limit of z* as z approaches 0 is path dependent, then you are wrong. The limit is 0.