- #1
Spinnor
Gold Member
- 2,216
- 430
In http://vixra.org/abs/1406.0172, the five-dimensional Kaluza-Klein line element d˜s^2 is given by,
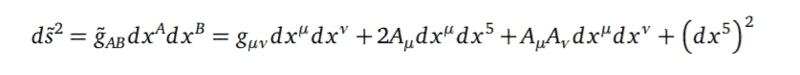
Does this look correct? Thanks!
Does this look correct? Thanks!
haushofer said:... There is no a priori reason why that element equals 1 as in your line element.
Spinnor said:Is there a reasonable argument that one could make to set it to 1 or if you set it to 1 what does that imply?
haushofer said:A nice playground without having to worry about strings is to compactify 6D GR on a torus or a spherical surface. You can see that if you add a Maxwell field to the theory and electromagnetic flux on the compact space, the moduli of the torus or sphere are stabilized.
Spinnor said:Does string theory then have something like a line element that might in some proper limit look like the line element above.
[URL='https://www.physicsforums.com/insights/author/urs-schreiber/']Urs Schreiber[/URL] said:In fact in pure gravity a KK-compactification with a small dilaton will collapse to a singularity in short time (Penrose 03, section 10.3).
viXra? Why is this paper in viXra? viXra is usually considered to be something like a crackpot version of arXiv. The paper above looks too good for viXra.Spinnor said:In http://vixra.org/abs/1406.0172, the five-dimensional Kaluza-Klein line element d˜s^2 is given by,
View attachment 207179
Does this look correct? Thanks!
There are also crackpots articles in arxiv; nowadays everyone can post something in the net.Demystifier said:viXra? Why is this paper in viXra? viXra is usually considered to be something like a crackpot version of arXiv. The paper above looks too good for viXra.
Fine, but if a serious scientist can choose to publish either in arXiv or viXra, what would make him to choose viXra and not arXiv? I cannot imagine any good reason.MathematicalPhysicist said:There are also crackpots articles in arxiv; nowadays everyone can post something in the net.
Just because everyone can post to vixra doesn't mean there aren't diamonds in it.
Demystifier said:Fine, but if a serious scientist can choose to publish either in arXiv or viXra, what would make him to choose viXra and not arXiv? I cannot imagine any good reason.
The Line element from Kaluza-Klein theory is a mathematical formula that represents the geometry of space-time in a five-dimensional universe, proposed by physicist Theodor Kaluza and mathematician Oskar Klein in the 1920s. It combines the equations of Einstein's theory of general relativity with the equations of electromagnetism to describe gravity and electromagnetism as two aspects of the same fundamental force.
The Line element is significant because it provides a way to unify the forces of gravity and electromagnetism, which were previously thought to be separate. This theory paved the way for future developments in unified field theories and the search for a theory of everything.
The Line element includes five dimensions - four dimensions of space and one dimension of time. This extra dimension is believed to be curled up or compactified, meaning it is too small for us to perceive, but it has a significant impact on the geometry of space-time and the laws of physics.
The Line element itself cannot be directly tested or observed, as it is a mathematical concept. However, the predictions of Kaluza-Klein theory, such as the existence of an extra dimension, can potentially be tested through experimental observations, such as particle accelerators or astronomical observations.
Yes, the Kaluza-Klein theory has been influential in the development of modern theories, such as string theory, which attempts to unify all of the fundamental forces of nature. It has also inspired new approaches to understanding the structure of space-time and the fundamental nature of the universe.