Line integral to calculate work

[Hernaner28]

Hi. I have a concrete doubt with this problem. Here's the pic.

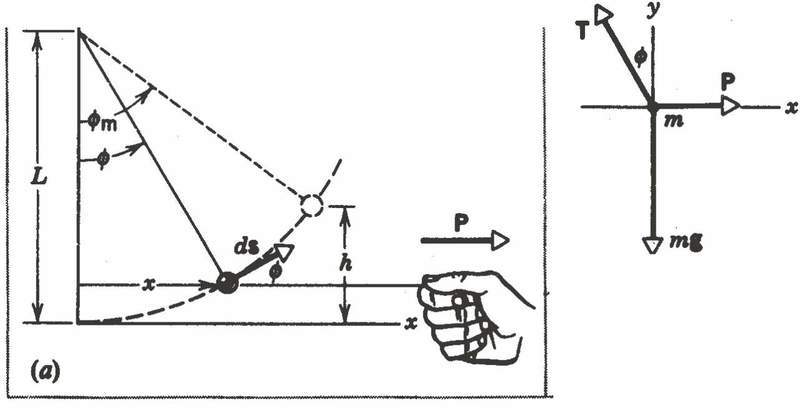
It asks me to calculate the work done by force P (the ball moves with constant speed). So the solution is in the book and I understood everything, but the problem comes here,

the force P in axis y is zero so the work of P should be:

\int\limits_{{x_o}}^{{x_f}} {{P_x}dx}

And we know that Px is equal to the tension in axis x so:

\int\limits_{}^{} {T\sin \theta dx}

But we need to convert the variable dx into theta variable. And the books states that as:
x = L\sin \theta
then:
dx = L\cos \theta d\theta

But shouldn't it be:
dx = L\sin\theta d\theta??

Why did it take the derivative of sine and not of x on the other side? Thank you!

 

[gneill]

Given:
$~~~x = L sin(\theta)$

Differentiate w.r.t. θ:
$~~~\frac{dx}{d \theta} = L cos(\theta)$

Rearrange:
$~~~dx = L cos(\theta) d\theta$

 

[Hernaner28]

Sorry but what did you do in the second step (wrt?)? I think I'm understaning now but I still don't get it.

Thanks!

 

[Whovian]

Differentiate both sides with respect to theta.

 

[Hernaner28]

Differentiate both sides with respect to theta.

Aham! So it would be an intermediate step there:

\frac{{dx}}{{d\theta }} = \frac{d}{{d\theta }}L\sin \theta

I didn't know that you could take dO to the other side as a product. Thanks!

 

[Whovian]

Think about it. If two functions are constantly the same, shouldn't their derivatives also be equal?

 

[Hernaner28]

And could this exercise be solved easily using the concepts of energy and conservative forces? Then, how could I begin?

Thanks!

Edit. I'll create a new thread.