Linear acceleration and angular acceleration

[thesandalman]

Homework Statement

How do I solve for linear acceleration or angular acceleration without one or the other?
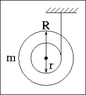
I am given the mass of the object (a yoyo), the inner radius, the outer radius, and Icm (moment of inertia at the center of mass).

Attached in a picture of the problem.

Homework Equations

a=alpha *r
alpha=a/r

The Attempt at a Solution

 

[rock.freak667]

The weight of the yo-yo produced a torque τ and if you did not know, τ = Iα, since you are given 'I', you can get 'α' and hence 'a' using your relevant equations.

 

[thesandalman]

How do you figure out the weight? Also the equation I have in my notes from the lecture, which I just double checked, is torque = I * alpha. Not I * a.

 

[rock.freak667]

How do you figure out the weight? Also the equation I have in my notes for the lecture, which I just double checked, is torque = I * alpha. Not I * a.

α = angular acceleration
a = linear acceleration


Weight is just 'mg'

 

[thesandalman]

I do not know if I am misunderstanding you or what, but that is not the correct answer.

 

[rock.freak667]

I do not know if I am misunderstanding you or what, but that is not the correct answer.

What did you have ?

 

[thesandalman]

i have torque is m*g*the outer radius = I* alpha but the answer I got was 651.7 alpha which does not make any sense for a yoyo.

 

[rock.freak667]

i have torque is m*g*the outer radius = I* alpha but the answer I got was 651.7 alpha which does not make any sense for a yoyo.

Can you post the values? Also the weight does not act there, it acts at through the center. So the weight is right at the start of the inner radius. So you used the wrong radius to get the torque.

 

[thesandalman]

A yoyo with a mass of m = 179 g.
The inner radius of the yoyo is r = 2.60 cm, and the outer radius is R = 3.60 cm
ICM = 9.70×10-5 kgm2

 

[rock.freak667]

Using the smaller radius does not give the correct answer?

 

[thesandalman]

nope.

 

[rock.freak667]

nope.

I now read that your inertia is at the center not where it rotates.

You need to use the parallel axis theorem I=I_cm +md² to get the inertia about the point where it rotates and then use the torque.