braindead101
- 158
- 0
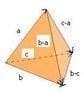
The figure below shows the tetrahedron determined by a,b,c E R^3. The area vector of a face is a vector perpendicular to the face, pointing outward, whose magnitude is the area of the face. Show that the sum of the four outward pointing area vectors of the faces equals the zero vector. I have attached the image.
Since the area of each face is identical can I just say it is some variable say c. So i am trying to look for the directional vector of each side.. but i am having trouble doing this. I think that vec b is one and vec (b-c) is another, but i am having trouble picturing the other two vectors especially the one pointing downwards.
Is this even the right approach to this problem?
Since the area of each face is identical can I just say it is some variable say c. So i am trying to look for the directional vector of each side.. but i am having trouble doing this. I think that vec b is one and vec (b-c) is another, but i am having trouble picturing the other two vectors especially the one pointing downwards.
Is this even the right approach to this problem?