Lelouch
- 18
- 0
A problem that I have to solve for my Linear Algebra course is the following
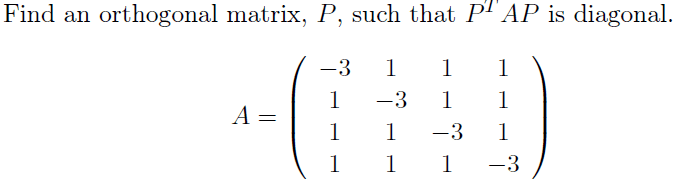
We are supposed to use Mathematica.
What I have done is that I first checked that A is symmetric, i.e. that ##A = A^T##. Which is obvious.
Next I computed the eigenvalues for A. The characteristic polynomial is given by ## det(A - \lambda*I) = \lambda(4+\lambda)^3 ##. Solving ## \lambda(4+\lambda)^3 = 0 ##, then yields the eigenvalues ## \lambda_1 = 0 ## and ## \lambda_2 = -4 ##. I used Mathematica to solve the determinant instead of doing it by hand. I also know that one could have used the Eigenvalues[] command in Mathematica. However, in order to report the step by step procedure in my report later I decided not to use the build in commands for Mathematica.
Next, I computed the eigenvectors for each eigenvalue. I.e. I computed ## (A - \lambda_i*I)* \vec x = \vec 0 ## for ## i = 1, 2 ##. I used mathematica to solve the matrices which yields the following eigenvectors.
For ## \lambda_1 = 0 ## we have ## \vec v_1 = (1, 1, 1, 1) ##.
For ## \lambda_2 = -4 ## we have ## \vec v_2 = (-1, 1, 0, 0), \vec v_3 = (-1, 0, 1, 0), \vec v_4 = (-1, 0, 0, 1)##.
I also checked the built in command Eigenvectors[] from Mathematica and it yields the same solution.
Next what I suppose had to be done is to use the Gram-Schmidt orthogonalization on ## \vec v_2, \vec v_3, \vec v_4 ##. This one I did not do by hand. Instead I used the command Orthogonalize[]. Which gave the vectors ## \vec w_2 = (-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0, 0), \vec w_3 = (-\frac{1}{\sqrt{6}}, -\frac{1}{\sqrt{6}}, \sqrt{\frac{2}{3}}, 0), \vec w_4 = (-\frac{1}{2\sqrt{3}}, -\frac{1}{2\sqrt{3}},
-\frac{1}{2\sqrt{3}}, \frac{\sqrt{3}}{2}) .##
I also normalized the vector ## \vec v_1 = (1, 1, 1, 1) ## which is then ## \vec w_1 = (\frac{1}{2}, \frac{1}{2}, \frac{1}{2}, \frac{1}{2}) ##.
Then, I formed the matrix ##P## such that
##P =
\begin{pmatrix}
\frac{1}{2} & -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{6}} & -\frac{1}{2\sqrt{3}} \\
\frac{1}{2} & \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{6}} & -\frac{1}{2\sqrt{3}} \\
\frac{1}{2} & 0 & \sqrt{\frac{2}{3}} & -\frac{1}{2\sqrt{3}} \\
\frac{1}{2} & 0 & 0 & \frac{\sqrt{3}}{2}
\end{pmatrix}
##.
After that I checked if ## P ## is an orthogonal matrix; i.e. ## P^T = P^{-1} ##. Which indeed turns out to be the case and also the Mathematica command OrthogonalMatrixQ[] gives true back.

Lastly, I wanted to compute the diagonal matrix ## D ## by ##P^T * A * P = D##. But this turns out rather strange in Mathematica:
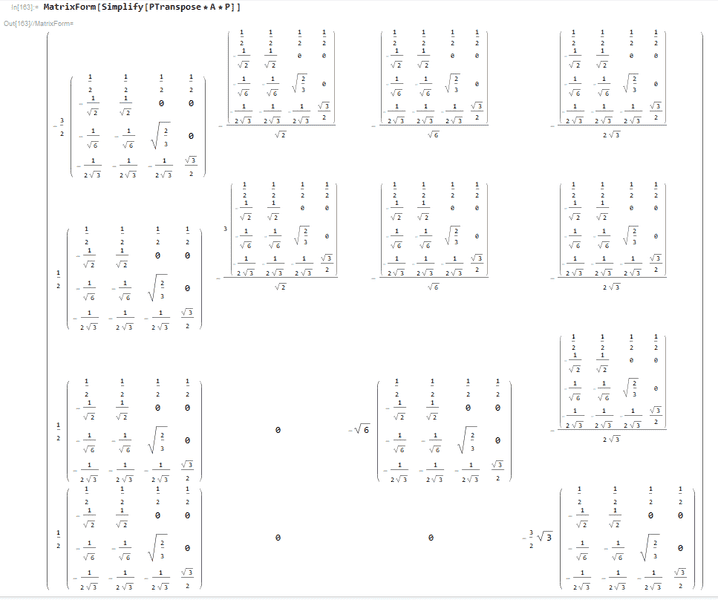
I am not sure what to make of this last result. I suppose I have made a mistake somewhere during the Gram-Schmidt Orthogonal Process. However, I cannot seem to find the mistake, if there is one. Also note that this is my first day working with Mathematica and the Gram-Schmidt Process.
We are supposed to use Mathematica.
What I have done is that I first checked that A is symmetric, i.e. that ##A = A^T##. Which is obvious.
Next I computed the eigenvalues for A. The characteristic polynomial is given by ## det(A - \lambda*I) = \lambda(4+\lambda)^3 ##. Solving ## \lambda(4+\lambda)^3 = 0 ##, then yields the eigenvalues ## \lambda_1 = 0 ## and ## \lambda_2 = -4 ##. I used Mathematica to solve the determinant instead of doing it by hand. I also know that one could have used the Eigenvalues[] command in Mathematica. However, in order to report the step by step procedure in my report later I decided not to use the build in commands for Mathematica.
Next, I computed the eigenvectors for each eigenvalue. I.e. I computed ## (A - \lambda_i*I)* \vec x = \vec 0 ## for ## i = 1, 2 ##. I used mathematica to solve the matrices which yields the following eigenvectors.
For ## \lambda_1 = 0 ## we have ## \vec v_1 = (1, 1, 1, 1) ##.
For ## \lambda_2 = -4 ## we have ## \vec v_2 = (-1, 1, 0, 0), \vec v_3 = (-1, 0, 1, 0), \vec v_4 = (-1, 0, 0, 1)##.
I also checked the built in command Eigenvectors[] from Mathematica and it yields the same solution.
Next what I suppose had to be done is to use the Gram-Schmidt orthogonalization on ## \vec v_2, \vec v_3, \vec v_4 ##. This one I did not do by hand. Instead I used the command Orthogonalize[]. Which gave the vectors ## \vec w_2 = (-\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0, 0), \vec w_3 = (-\frac{1}{\sqrt{6}}, -\frac{1}{\sqrt{6}}, \sqrt{\frac{2}{3}}, 0), \vec w_4 = (-\frac{1}{2\sqrt{3}}, -\frac{1}{2\sqrt{3}},
-\frac{1}{2\sqrt{3}}, \frac{\sqrt{3}}{2}) .##
I also normalized the vector ## \vec v_1 = (1, 1, 1, 1) ## which is then ## \vec w_1 = (\frac{1}{2}, \frac{1}{2}, \frac{1}{2}, \frac{1}{2}) ##.
Then, I formed the matrix ##P## such that
##P =
\begin{pmatrix}
\frac{1}{2} & -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{6}} & -\frac{1}{2\sqrt{3}} \\
\frac{1}{2} & \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{6}} & -\frac{1}{2\sqrt{3}} \\
\frac{1}{2} & 0 & \sqrt{\frac{2}{3}} & -\frac{1}{2\sqrt{3}} \\
\frac{1}{2} & 0 & 0 & \frac{\sqrt{3}}{2}
\end{pmatrix}
##.
After that I checked if ## P ## is an orthogonal matrix; i.e. ## P^T = P^{-1} ##. Which indeed turns out to be the case and also the Mathematica command OrthogonalMatrixQ[] gives true back.
Lastly, I wanted to compute the diagonal matrix ## D ## by ##P^T * A * P = D##. But this turns out rather strange in Mathematica:
I am not sure what to make of this last result. I suppose I have made a mistake somewhere during the Gram-Schmidt Orthogonal Process. However, I cannot seem to find the mistake, if there is one. Also note that this is my first day working with Mathematica and the Gram-Schmidt Process.
Attachments
Last edited:

