Magnet moved through copper ring

[Padenton]

Homework Statement

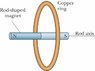
The figure shows a ring of copper with its plane perpendicular to the axis of the nearby rod-shaped magnet. For each of the situations described below, indicate whether there will or will not be a current induced in the ring and justify your reasoning, drawing pictures if necessary.

The magnet is moved horizontally toward the left?
The ring is moved away from the magnet?
The ring is rotated around any of its diameters?
The magnet is moved up or down?
The ring is rotated around its center in the plane in which it lies?

Homework Equations

ΔFlux=Induced Current

The Attempt at a Solution

The magnet is moved horizontally toward the left?
Yes, there will be a change in flux so a current will be induced.

The ring is moved away from the magnet?
Yes, there will be a change in flux so a current will be induced.

The ring is rotated around any of its diameters?
No, there would not be a change in flux so no current will be induced.

The magnet is moved up or down?
No, there would not be a change in flux so no current will be induced.

The ring is rotated around its center in the plane in which it lies?
Yes, there will be a change in flux similar to if the magnet rotated, therefore a current will be induced.

Im not sure how correct my reasoning or answers are, any explanation or help would be much appreciated. Thank you

 

[Spinnor]

I think your third, fourth, and fifth answers are wrong. See sketch for #3. For number 4 I suspect there is a clever hand waving argument but I can't think of it right now so I got a large coil of wire, a magnet, and a digital volt meter and seemed to confirm my hunch that the movement in question 4 should generate induced current, not a large one though compared with the others. For number 5 the integral of BdotA does not change in time so there is no induced current.