Magnetic Field Due to a Curved Wire Segment

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

The solution is,

However, why did they not use limits of integration for the integral in red? When I solved this, I used

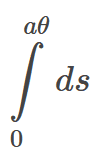
as limits of integration.

I see that is not necessary since you get the same answer either way, but is there a deeper reason?

Many thanks!

 

[haruspex]

The text says "integrate over the curved path AC", so it was not essential to write that in the algebra. Also, one does not always have to specify the integration domain as a pair of endpoints. They could have defined S as the curve AC and written $\int_S$.

 

[member 731016]

The text says "integrate over the curved path AC", so it was not essential to write that in the algebra. Also, one does not always have to specify the integration domain as a pair of endpoints. They could have defined S as the curve AC and written $\int_S$.

Thanks for your help @haruspex ! That second notation you mention makes more sense than their single integral over ds. I think another way to avoid implicitly defining an integration domain is by using a line integral

to denote that we are summing the length elements over the path, correct?

 

[haruspex]

Thanks for your help @haruspex ! That second notation you mention makes more sense than their single integral over ds. I think another way to avoid implicitly defining an integration domain is by using a line integral View attachment 320352to denote that we are summing the length elements over the path, correct?

No, that symbol is for integrating around a closed loop.

 

[member 731016]

No, that symbol is for integrating around a closed loop.

Oh, thank you for your help @haruspex !