Magnetic field of solenoid and a coil with multiple turns

[rooks]

Hi!,

I have a question for you geniuses (geniusi?)

Why are there two different equations to find the magnetic field of a solenoid and a coil with multiple turns?

(According to my textbook)
The equations for each are
Solenoid:

Coil with multiple turns:

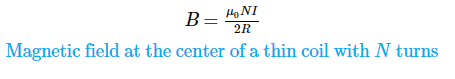
Why are they different? Is there a physical difference between a coil and a solenoid?Thanks for the help.

 

[BvU]

Hello Rooks,

Don't double-post, please.
And google a bit before you post: your expressions apply to different kinds of coil: the first one for a long coil
the second for a very short coil

[edit] Google is your friend. Maybe you'll like section 9.4 here

 

[rooks]

Hello Rooks,

Don't double-post, please.
And google a bit before you post: your expressions apply to different kinds of coil: the first one for a long coil
the second for a very short coil

Ok, then where is the threshold? When does a coil become too long to use the 2nd equation? When does a solenoid become too short to use the 1st equation?

Also, I meant why does the length matter and make the equation different?

 

[BvU]

Ok, then where is the threshold?

No threshold but a gradual transition.
There is an intermediate range where neither can be used. The first one stops being useful if the solid angle of the end turn becomes too large.
The second one stops being useful if it's significantly lower than 2 $\pi$.

 

[rude man]

You have to use Biot-Savart for "short" coils. You can use Biot-Savart for "long" coils but Ampere's law is usually OK.

You can use Ampere's law if the length of the coil is long enough to warrant ignoring the B field outside the coil.

As BvU say, there is a transition.

And BTW both approaches allow you to determine the B field on the axis, nowhere else.