Magnetic Field Reflection from a Media Interface

[SeriousTyro]

Say there is an electric field oriented along the x-axis and is propagating along the z-axis. A medium exists from z>0.

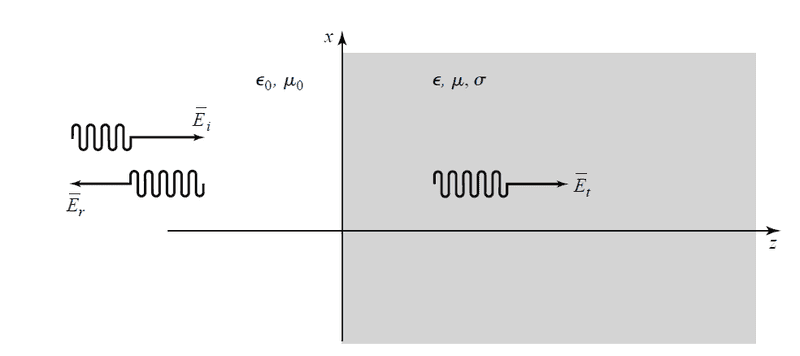
The fields for z<0 can be written as

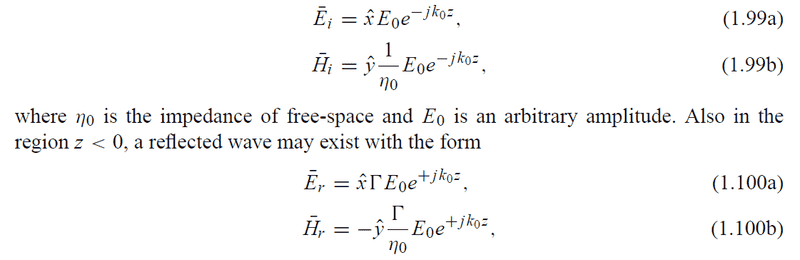
I'm confused on the negative sign of the reflected magnetic field.

 

[mfb]

This is not a propagating electric field, it is a propagating electromagnetic wave.

The relative orientation between electric and magnetic field is linked to the propagation direction. To flip the propagation direction (which you do for the reflection), you have to switch the relative orientation. This is done with the minus sign.

 

[SredniVashtar]

It is easier to see in 3D: imagine a triad E H k (where k is the wave vector - or if you prefer you could use the Poynting vector S = E x H) impinging on the surface at an angle theta. The field that is tangential to the surface is the same in the incident and reflected wave, so the other field has to adapt in order to give the correct direction for S (or k). You can simulate this with your right hand: thumb is E, index is H, middle finger is k, put them at right angles and move it against a wall in the direction of the middle finger. The reflected 'hand' should also move in the direction of the middle finger: you will see that if you must mantain the direction of your thumb, your index will point in the opposite direction (if incidence is perpendicular, or somewhat in the other way for oblique incidence).

A more general description should distinguish between TE and TM modes and analyze the boundary conditions case by case at the interface (conservation of the tangential or normal field is a consequence of Maxwell's equations with given boundary conditions. Basically, you prove it by means of a small loop for conservative fields, and a small closed surface for solenoidal fields).