Jnumen
- 2
- 0
Homework Statement
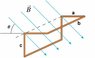
A 10cm x 10cm square is bent at a 90deg angle as shown in the figure.
A uniform 0.050T magnetic field points downdard at 45deg.
What is the magnetic flux through the loop.
Homework Equations
Flux= [(Aeff)*(B)].
Flux= [(Aeff)*(B)]*cos(theta).
The Attempt at a Solution
First I solved for the side due to the bend by using d= SQRT of [(a)^2*(c)^2].
Then, I calculated the Area using A= [(d)*(b)].
Then, I tried calculating with or without the 45deg angle using the following (which is not giving the correct answer):
Flux= [(Aeff)*(B)].
Flux= [(Aeff)*(B)]*cos(theta).