Magnitude and direction question

AI Thread Summary
To determine the magnitudes and directions of the forces exerted by the chain and bracket supporting a 495N sign, it's essential to analyze the forces involved using trigonometric functions. The discussion suggests using the law of sines or cosines, depending on the angles present in the problem. Participants emphasize the need for a clear description of the setup to provide accurate guidance. Understanding the constraints, such as the horizontal rod's inability to support vertical forces, is crucial for solving the problem. A detailed illustration or description of the angles and configuration would greatly assist in setting up the calculations.
Peacehomes
Messages
1
Reaction score
0
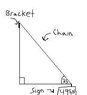
"A sign weighting 495N is supported as shown in the attachment. Determine the magnitudes and directions of the forces exerted by the chain and by the bracket. assume that the horizontal rod cannot support vertical forces."


How do I set up this question? Do I use the law of Sins? Cos?

I really hate learning from the book, and since the book didn't show an example of this type of problem I don't really know where to start. Not asking for the solution, just a little kick start help. Thanks
 

Attachments

  • untitled.JPG
    untitled.JPG
    4.7 KB · Views: 429
Physics news on Phys.org
cant see the jpg but if the angle is mentoined then you could use sins and cosines and then do the rest...
 
Describe the illustration in a little more detail
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »

Similar threads

Vector problem, magnitude of the force
Replies
30
Views
2K
Find the direction and the magnitude of Frictional force
Replies
3
Views
758
To find direction and magnitude of forces acting in a system
Replies
2
Views
1K
Intuition on the direction of friction in a rotational dynamics problem
Replies
13
Views
2K
Calculate the magnitude and direction of the torque
Replies
1
Views
2K
Calculating Net Force on a Wheel: Magnitude and Direction | 0.350 m Radius
Replies
4
Views
2K
Statics problem on the resolution of forces
Replies
18
Views
2K
Find the magnitude of the electric field at point P
Replies
5
Views
2K
Electrostatics? Magnitude and direction of a magnetic field
Replies
4
Views
2K
Newton's Third Law for book on a table
Replies
8
Views
3K

Hot Threads

Recent Insights

Back
Top