Magnitude of the induced magnetic field in a circuit

[L_landau]

Homework Statement

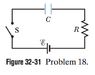
The circuit in Fig. 32-31 consists of switch S, a 12.0 V ideal battery, a 20.0 M resistor, and an air-filled capacitor. The capacitor has parallel circular plates of radius 5.00 cm, separated by 3.00mm. At time t=0, switch S is
closed to begin charging the capacitor. The electric field between the plates is uniform. At t=250 ms, what is the magnitude of the magnetic field within the capacitor, at radial distance 3.00 cm?

Homework Equations

∫ B⋅ds = ε₀ dφ_E/dt

The Attempt at a Solution

I started by looking at dφ_E/dt. I said dφ_E/dt = dE/dt * A. Then I said that q = CV and therefore dq/dt = C dV/dt --> dv/dt = I/C. For a parallel plate capacitor we know that ΔV = E*d so taking the derivative dV/dt = dE/dt*d -- > dE/dt = 1/d * dV/dt. I then plug in the previously found dV/dt (=I/C) and since for a parallel capacitor C = ε₀ * A/d, dE/dt = 1/d * I*d/ε₀*A = I/(ε₀*A). I'm quite confused because this gives me units of A*Newtons*m^2/coulombs^2, which is V/m/s. This seems dimensionally incorrect to me. Could anyone point me in the right direction?

 

[TSny]

dE/dt = ... = I/(ε₀*A).

OK

I'm quite confused because this gives me units of A*Newtons*m^2/coulombs^2,

This isn't quite right. Looks like you forgot to include the units for the area.

... which is V/m/s. This seems dimensionally incorrect to me.

You should find the units to be V/(m⋅s). Recall that the SI unit for E can be written V/m.

You can see that to find dE/dt at some time t, you will need the current at that time. You probably covered equations for charging a capacitor in an RC circuit that would be helpful here.

 

[L_landau]

Ah I see. I was getting a different answer when I finished that line of reasoning but I just realized that it's because the magnetic field generated is supposed to be from the current ∫B⋅ds=μ₀ I_enc rather than from a change in electric flux. This is kind of confusing to me because I thought that when a capacitor is being charged we say that there's a change of flux that induces a B-field. Any insight?

 

[TSny]

Your original approach looks good to me. B is due to the changing flux of E. I just noticed that your equation ∫ B⋅ds = ε₀ dφ_E/dt in your first post is missing a factor of μ₀.

You can think of the equation ∫B⋅ds=μ₀ I_enc as applying if you interpret I_enc as the "displacement current" enclosed. But the displacement current is defined as ε₀ dφ_E/dt.

 

[L_landau]

so finishing this problem I have
I = (ε/R)e^-t/RC --> ∫B⋅ds = μ₀ (ε/R) e^-t/RC. This leads to
B = μ₀/(2πr) (ε/R) e^-t/RC which for the time given leads to B = 2.34x10^-12, but the correct answer is 8.4x10^-13. Any ideas where I could be going wrong? The answer just uses B = μ₀ i_d r / (2πR²) for the magnetic field inside of wires. The i_d is the displacement current.

 

[TSny]

so finishing this problem I have
I = (ε/R)e^-t/RC --> ∫B⋅ds = μ₀ (ε/R) e^-t/RC.

Here you are using the total current I going into the capacitor.

Instead, you need to use the displacement current through the appropriate area. You should think about what area constitutes the appropriate area. So, the current you need is I'_d =ε₀ dφ_E/dt where φ_E needs to be calculated for the appropriate area. I use a prime on I here to denote the displacement current through the appropriate area as opposed to the total displacement current I_d for the entire area of a plate. I_d (for the entire area of the plate) can be shown to equal the total current I going into the capacitor. But, I'_d is only a certain fraction of I_d.

If you set it up correctly, you should be able to show how the result is equivalent to the expression B = μ₀ i_d r / (2πR²)