Rafael de Gomes
- 1
- 0
Hello,
I've been trying to come up with a short way of writing the code. What I'm trying to do is:
I have 11 equations, each of which have a defined minimum and maximum. I'm trying to find the highest maximum out of all of them and I need to know which one it is. The highest as in farthest away from zero, so negative values are also required.
I was trying this:
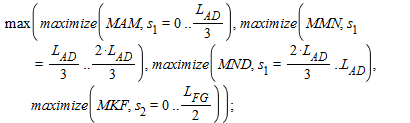
And although this would work (it does give me a value), it doesn't tell me which of the functions is the highest. Is there any way to do this other than wasting a bunch of lines writing:
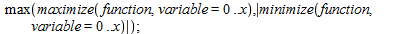
?
I've been trying to come up with a short way of writing the code. What I'm trying to do is:
I have 11 equations, each of which have a defined minimum and maximum. I'm trying to find the highest maximum out of all of them and I need to know which one it is. The highest as in farthest away from zero, so negative values are also required.
I was trying this:
And although this would work (it does give me a value), it doesn't tell me which of the functions is the highest. Is there any way to do this other than wasting a bunch of lines writing:
?