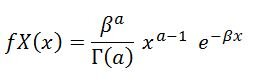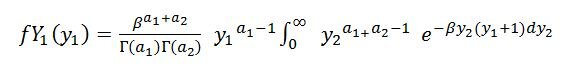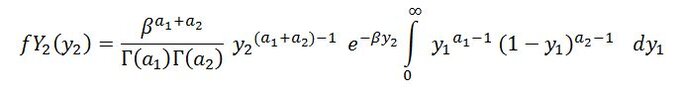Marginal probability density functions (pdf)

[QuebecRb]

I have a set of two related queries relating to marginal pdfs:
i.How to proceed finding the marginal pdfs of two independent gamma distributions (X1 and X2) with parameters (α1,β) and (α2,β) respectively, given the transformation: Y1=X1/(X1+X2) and Y2=X1+X2.
I am using the following gamma formula:

View attachment 3407

Having written the joint pdf and having applied the Jacobean, I have reached the final stage of writing the expression for the marginal (Y1):

View attachment 3408

but I cannot proceed further, obtaining the marginal pdf.

ii.Additionally, given the following transformations , Y1=X1/X2 and Y2=X2, I have written the expression for the marginal (Y2):

View attachment 3409

How do I find this marginal pdf?

Any enlightening answers would be appreciated.

 

[Siron]

I'm a little bit confused about the exercice. If I understand it correctly, you have given two independent gamma distributed random variables $X_1 \sim \Gamma(\alpha_1, \beta) $ and $X_2 \sim \Gamma(\alpha_2,\beta) $ and the goal is to compute the distribution of $Y_1 = \frac{X_1}{X_1+X_2}$ and $Y_2 = X_1+X_2$. Am I right here?

I did not check if your solution for $f_{Y_1}(y_1)$ and $f_{Y_2}(y_2)$ is correct, but to proceed the Gamma function can be useful. It is defined as
$$\Gamma(z) = \int_{0}^{\infty} t^{z-1}e^{-t}dt$$

For example to compute the following integral
$$\int_{0}^{\infty} y_2^{\alpha_1+\alpha_2-1}e^{-\beta y_2(y_1+1)}dy_2 $$

Let $\beta y_2(y_1+1) = t \Rightarrow dy_2 = \frac{dt}{\beta(y_1+1)}$. Thus the integral becomes
$$\frac{1}{\beta (y_1+1)} \int_{0}^{\infty} \left[\frac{t}{\beta(y_1+1)}\right]^{\alpha_1+\alpha_2-1} e^{-t}dt = \frac{1}{\beta^{\alpha_1+\alpha_2}(y_1+1)^{\alpha_1+\alpha_2}} \int_{0}^{\infty} t^{\alpha_1+\alpha_2-1}e^{-t}dt = \frac{1}{\beta^{\alpha_1+\alpha_2}(y_1+1)^{\alpha_1+\alpha_2}} \Gamma(\alpha_1+\alpha_2)$$