Markov Chains and Limit question : Where have I gone wrong?

[Firepanda]

I am doing question 2 here:

My solution so far is this:

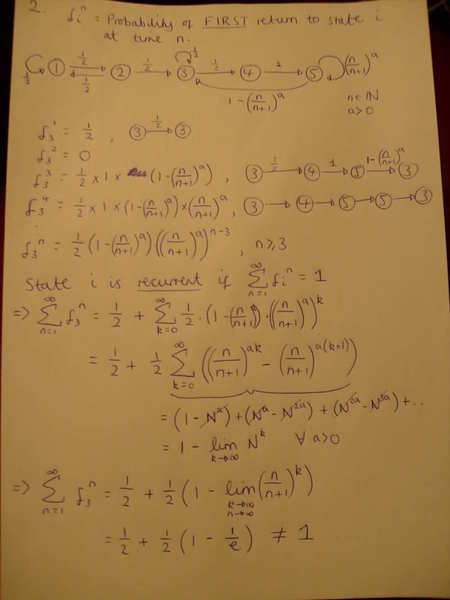
Where have I gone wrong? I'm assuming I'm taking the wrong limit but I'm really stumped here and no idea what else it should be..

I hope my writing is ok, I tried to be as neat as possible!

Thanks

 

[TheFurryGoat]

Your indexes k and n are not independent, but it looks like you have "independent" limits and terms in the sums, although I believe you have taken the limit with k = n. If I understood correctly, you should have k = n-3. If you plug this in you should get something else.

 

[Firepanda]

I did initially have k = n-3, but I swapped to k because I thought the n's on the LHS and the RHS were different (and independant), and it was confusing me.

Putting k = n-3 does it really change anything? I can't see what it changes..

Thanks

 

[TheFurryGoat]

I'm sorry, it doesn't change a thing. But now I noticed that the sum isn't calculated correctly, you should change k back to n-3 so you can see the flaw. The sum is actually
$\sum_{n=3}^{\infty}\left(\frac{n}{n+1}\right)^{a(n-3)}-\left(\frac{n}{n+1}\right)^{a(n-2)}$ so the cancellations are not correct.

 

[Firepanda]

I'm sorry, it doesn't change a thing. But now I noticed that the sum isn't calculated correctly, you should change k back to n-3 so you can see the flaw. The sum is actually
$\sum_{n=3}^\infty{\left(\frac{n}{n+1}\right)^{a(n-3)}-\left(\frac{n}{n+1}\right)^{a(n-2)}$ so the cancellations are not correct.

starting at n=3 I get (1 - N^a) : n=4 I get (N^a - N^2a)

etc

Isn't it the same cancellation?

 

[TheFurryGoat]

Aren't consecutive terms at indexes n, n+1 like so:

$a_n= \left(\frac{n}{n+1}\right)^{a(n-3)}-\left(\frac{n}{n+1}\right)^{a(n-2)}$
$a_{n+1}= \left(\frac{n+1}{n+2}\right)^{a(n-2)}-\left(\frac{n+1}{n+2}\right)^{a(n-1)}$?

 

[Firepanda]

Aren't consecutive terms at indexes n, n+1 like so:

$a_n= \left(\frac{n}{n+1}\right)^{a(n-3)}-\left(\frac{n}{n+1}\right)^{a(n-2)}$
$a_{n+1}= \left(\frac{n+1}{n+2}\right)^{a(n-2)}-\left(\frac{n+1}{n+2}\right)^{a(n-1)}$?

Ah of course, woops!

where do I go from here, I assume I can't cancel any of them, right?

Not sure how to sum that series either..

 

[TheFurryGoat]

Yes, it looks like a very tough series to me. I don't know where to go from there. I don't know anything about Markov chains so I don't know how you calculate the $f_n^i$ 's. Did you calculate them by $T^{(n)}=T(1)\cdots T(n)?$
cause it looks to me like you should have $f_3^3 = 1/2 \cdot 1 \cdot (1-\frac{3}{3+1})^a$
$f_3^4 = 1/2 \cdot 1 \cdot (\frac{3}{3+1})^a \cdot (1-\frac{4}{4+1})^a$
$f_3^5 = 1/2 \cdot 1 \cdot (\frac{3}{3+1})^a \cdot (\frac{4}{4+1})^a \cdot (1-\frac{5}{5+1})^a$
and so forth. Mayby I'm not interpreting the probabilities correctly, as I said, I'm not familiar with these...

 

[Ray Vickson]

If the system is in state 5 at time n, the probability that it remains in state 5 at times n+1, n+2,...,n+k is
$$\left(\frac{n}{n+1}\right)^a \left(\frac{n+1}{n+2}\right)^a \cdots \left(\frac{n+k-1}{n+k}\right)^a = \left( \frac{n}{n+k}\right)^a,$$
which --> 0 as k --> infinity. You can fix up this argument to show that $\Pr \{ X_{n+k}=5 \; \mbox{ i.o. } |X_n = 5 \} = 0,$, so state 5 is left with probability 1 at a finite time. When that happens, the system returns to state 3, implying that state 3 is recurrent.

RGV

 

[TheFurryGoat]

If it is calculated like I suspect it is, then you will get a satisfying answer.
So first we want to find out what $f_3^n$ is when $n\geq 3:$

$f_3^n = \displaystyle \frac{1}{2}\cdot1\cdot\left(\prod_{k=3}^{n-1}\left(\frac{k}{k+1}\right)^a\right)\cdot\left(1-\left(\frac{n}{n+1}\right)^a\right) = \frac{1}{2}\cdot\left(\frac{(n-1)!}{2}\cdot\frac{2\cdot3}{n!}\right)^a\cdot\left(1-\left(\frac{n}{n+1}\right)^a\right)$
$\displaystyle = \frac{1}{2} \cdot \left( \frac{3}{n} \right)^a \cdot \left(1-\left( \frac{n}{n+1} \right)^a \right) = \frac{3^a}{2} \cdot \left(\frac{1}{n^a}- \frac{1}{(n+1)^a}\right)$
So now the sum of the probabilities is easy to calculate, and I believe that you will finally get the correct answer.