- #1
rocapp
- 95
- 0
Homework Statement
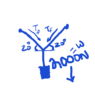
A mass of 200 kg is hanging directly in the center of a chain; the chain makes a 20o angle from its horizontal. The chain will break if more than 2000 N of force are applied at any point on the chain. Will the chain break?
Homework Equations
F=ma
Tfy=mg(sin[itex]\Theta[/itex])
g=10m/s
The Attempt at a Solution
2000N = 2Tf(sin20)
Tf1 = 1000/sin20
Tf1 = 1095 N
Tf2 = 1095 N
Tftotal = 1095N + 1095N
Tftotal = 2190 N
The chain will break.
 I assume the "2000 N" comes from mg = (200 [kg])(10 [m/s2]) = 2000 N. So far so good.
I assume the "2000 N" comes from mg = (200 [kg])(10 [m/s2]) = 2000 N. So far so good.